Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 57357 by ANTARES VY last updated on 03/Apr/19

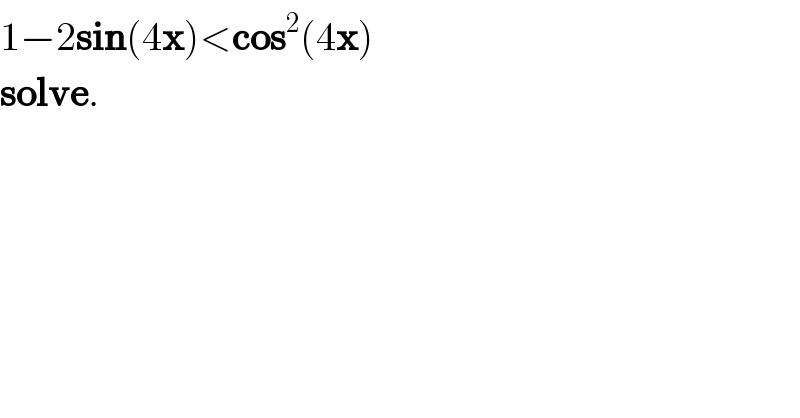
1−2sin(4x)<cos^2 (4x) solve.

$$\mathrm{1}−\mathrm{2}\boldsymbol{\mathrm{sin}}\left(\mathrm{4}\boldsymbol{\mathrm{x}}\right)<\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\mathrm{4}\boldsymbol{\mathrm{x}}\right) \\ $$ $$\boldsymbol{\mathrm{solve}}. \\ $$

Commented bybshahid010@gmail.com last updated on 03/Apr/19

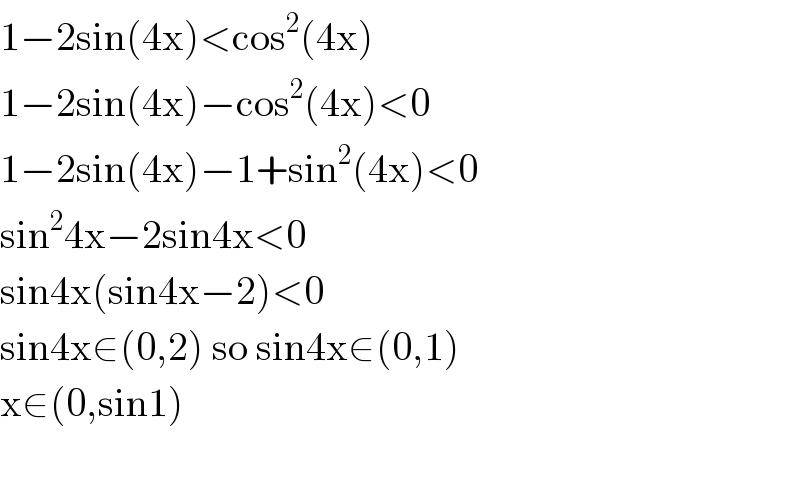
1−2sin(4x)<cos^2 (4x) 1−2sin(4x)−cos^2 (4x)<0 1−2sin(4x)−1+sin^2 (4x)<0 sin^2 4x−2sin4x<0 sin4x(sin4x−2)<0 sin4x∈(0,2) so sin4x∈(0,1) x∈(0,sin1)

$$\mathrm{1}−\mathrm{2sin}\left(\mathrm{4x}\right)<\mathrm{cos}^{\mathrm{2}} \left(\mathrm{4x}\right) \\ $$ $$\mathrm{1}−\mathrm{2sin}\left(\mathrm{4x}\right)−\mathrm{cos}^{\mathrm{2}} \left(\mathrm{4x}\right)<\mathrm{0} \\ $$ $$\mathrm{1}−\mathrm{2sin}\left(\mathrm{4x}\right)−\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{4x}\right)<\mathrm{0} \\ $$ $$\mathrm{sin}^{\mathrm{2}} \mathrm{4x}−\mathrm{2sin4x}<\mathrm{0} \\ $$ $$\mathrm{sin4x}\left(\mathrm{sin4x}−\mathrm{2}\right)<\mathrm{0} \\ $$ $$\mathrm{sin4x}\in\left(\mathrm{0},\mathrm{2}\right)\:\mathrm{so}\:\mathrm{sin4x}\in\left(\mathrm{0},\mathrm{1}\right) \\ $$ $$\mathrm{x}\in\left(\mathrm{0},\mathrm{sin1}\right) \\ $$ $$ \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 03/Apr/19

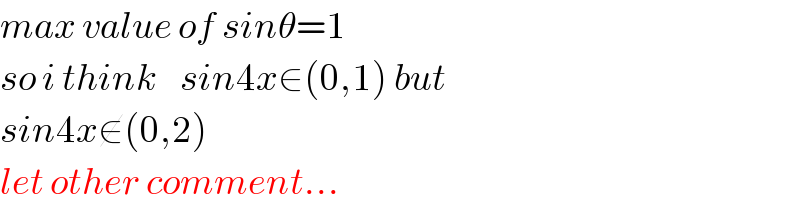
max value of sinθ=1 so i think sin4x∈(0,1) but sin4x∉(0,2) let other comment...

$${max}\:{value}\:{of}\:{sin}\theta=\mathrm{1}\: \\ $$ $${so}\:{i}\:{think}\:\:\:\:{sin}\mathrm{4}{x}\in\left(\mathrm{0},\mathrm{1}\right)\:{but}\: \\ $$ $${sin}\mathrm{4}{x}\notin\left(\mathrm{0},\mathrm{2}\right)\: \\ $$ $${let}\:{other}\:{comment}... \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19

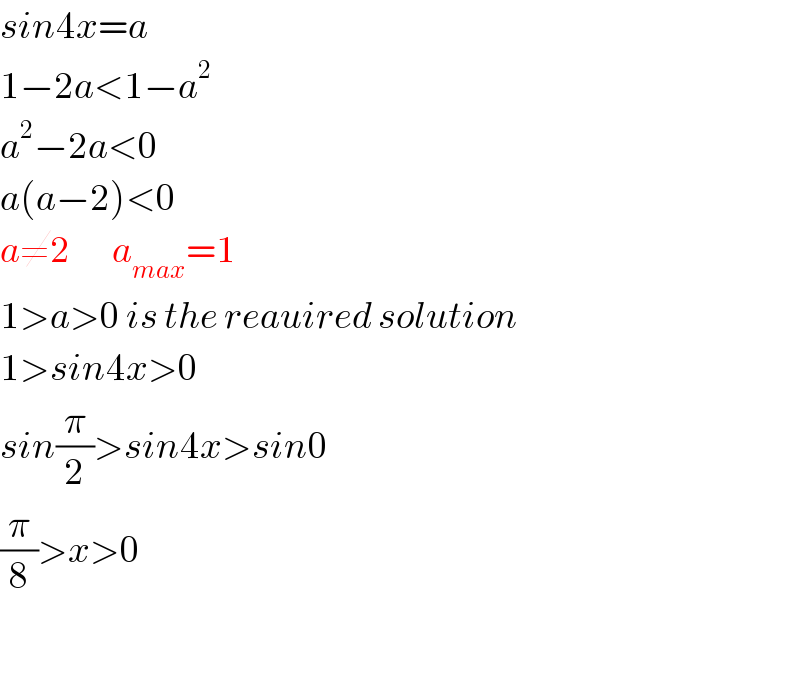
sin4x=a 1−2a<1−a^2 a^2 −2a<0 a(a−2)<0 a≠2 a_(max) =1 1>a>0 is the reauired solution 1>sin4x>0 sin(π/2)>sin4x>sin0 (π/8)>x>0

$${sin}\mathrm{4}{x}={a} \\ $$ $$\mathrm{1}−\mathrm{2}{a}<\mathrm{1}−{a}^{\mathrm{2}} \\ $$ $${a}^{\mathrm{2}} −\mathrm{2}{a}<\mathrm{0} \\ $$ $${a}\left({a}−\mathrm{2}\right)<\mathrm{0} \\ $$ $${a}\neq\mathrm{2}\:\:\:\:\:\:\:{a}_{{max}} =\mathrm{1} \\ $$ $$\mathrm{1}>{a}>\mathrm{0}\:{is}\:{the}\:{reauired}\:{solution}\: \\ $$ $$\mathrm{1}>{sin}\mathrm{4}{x}>\mathrm{0} \\ $$ $${sin}\frac{\pi}{\mathrm{2}}>{sin}\mathrm{4}{x}>{sin}\mathrm{0} \\ $$ $$\frac{\pi}{\mathrm{8}}>{x}>\mathrm{0} \\ $$ $$ \\ $$

Commented byANTARES VY last updated on 03/Apr/19

???

$$??? \\ $$

Answered by einsteindrmaths@hotmail.fr last updated on 03/Apr/19

cos^2 (4x)=1−sin^2 (4x)====>1−sin(4x)<1−sin^2 (4x) ==>sin^2 (4x)−sin(4x)<0==>sin(4x)(1−sin(4x))<0==> sin(4x)>0&1−sin(4x)≠0===>x≠{(π/8)+((kπ)/2)/k∈IZ}∪]((kπ)/(2 ));(((2k+1)π)/4)[

$${c}\mathrm{os}\:^{\mathrm{2}} \left(\mathrm{4}{x}\right)=\mathrm{1}−{sin}^{\mathrm{2}} \left(\mathrm{4}{x}\right)====>\mathrm{1}−\mathrm{sin}\left(\mathrm{4}{x}\right)<\mathrm{1}−{sin}^{\mathrm{2}} \left(\mathrm{4}{x}\right) \\ $$ $$==>{sin}^{\mathrm{2}} \left(\mathrm{4}{x}\right)−{sin}\left(\mathrm{4}{x}\right)<\mathrm{0}==>{sin}\left(\mathrm{4}{x}\right)\left(\mathrm{1}−{sin}\left(\mathrm{4}{x}\right)\right)<\mathrm{0}==> \\ $$ $$\left.{sin}\left(\mathrm{4}{x}\right)>\mathrm{0\&1}−{sin}\left(\mathrm{4}{x}\right)\neq\mathrm{0}===>{x}\neq\left\{\frac{\pi}{\mathrm{8}}+\frac{{k}\pi}{\mathrm{2}}/{k}\in{IZ}\right\}\cup\right]\frac{{k}\pi}{\mathrm{2}\:};\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}}\left[\right. \\ $$

Answered by mr W last updated on 03/Apr/19

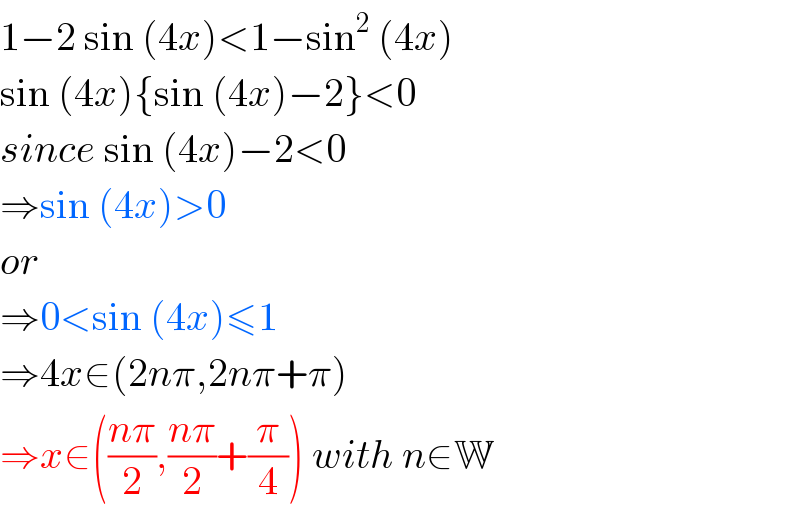
1−2 sin (4x)<1−sin^2 (4x) sin (4x){sin (4x)−2}<0 since sin (4x)−2<0 ⇒sin (4x)>0 or ⇒0<sin (4x)≤1 ⇒4x∈(2nπ,2nπ+π) ⇒x∈(((nπ)/2),((nπ)/2)+(π/4)) with n∈W

$$\mathrm{1}−\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{4}{x}\right)<\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{4}{x}\right) \\ $$ $$\mathrm{sin}\:\left(\mathrm{4}{x}\right)\left\{\mathrm{sin}\:\left(\mathrm{4}{x}\right)−\mathrm{2}\right\}<\mathrm{0} \\ $$ $${since}\:\mathrm{sin}\:\left(\mathrm{4}{x}\right)−\mathrm{2}<\mathrm{0} \\ $$ $$\Rightarrow\mathrm{sin}\:\left(\mathrm{4}{x}\right)>\mathrm{0} \\ $$ $${or} \\ $$ $$\Rightarrow\mathrm{0}<\mathrm{sin}\:\left(\mathrm{4}{x}\right)\leqslant\mathrm{1} \\ $$ $$\Rightarrow\mathrm{4}{x}\in\left(\mathrm{2}{n}\pi,\mathrm{2}{n}\pi+\pi\right) \\ $$ $$\Rightarrow{x}\in\left(\frac{{n}\pi}{\mathrm{2}},\frac{{n}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\:{with}\:{n}\in\mathbb{W} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com