
Question Number 57012 by rahul 19 last updated on 28/Mar/19
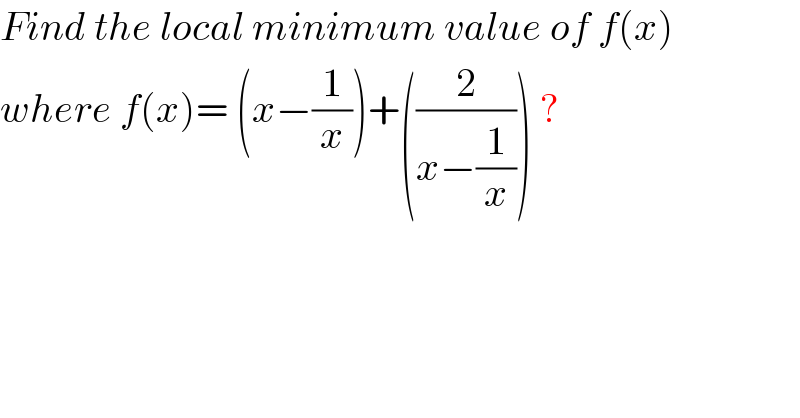
$${Find}\:{the}\:{local}\:{minimum}\:{value}\:{of}\:{f}\left({x}\right) \\ $$$${where}\:{f}\left({x}\right)=\:\left({x}−\frac{\mathrm{1}}{{x}}\right)+\left(\frac{\mathrm{2}}{{x}−\frac{\mathrm{1}}{{x}}}\right)\:? \\ $$
Answered by mr W last updated on 29/Mar/19
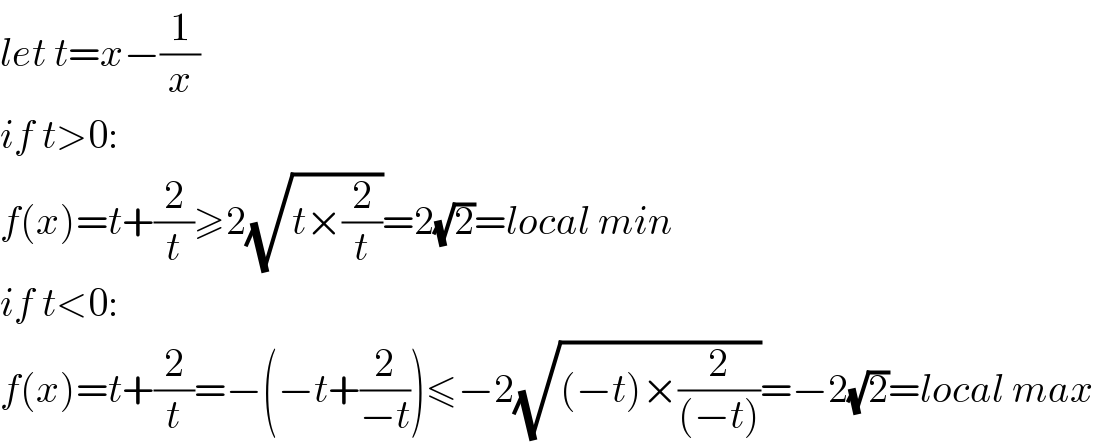
$${let}\:{t}={x}−\frac{\mathrm{1}}{{x}} \\ $$$${if}\:{t}>\mathrm{0}: \\ $$$${f}\left({x}\right)={t}+\frac{\mathrm{2}}{{t}}\geqslant\mathrm{2}\sqrt{{t}×\frac{\mathrm{2}}{{t}}}=\mathrm{2}\sqrt{\mathrm{2}}={local}\:{min} \\ $$$${if}\:{t}<\mathrm{0}: \\ $$$${f}\left({x}\right)={t}+\frac{\mathrm{2}}{{t}}=−\left(−{t}+\frac{\mathrm{2}}{−{t}}\right)\leqslant−\mathrm{2}\sqrt{\left(−{t}\right)×\frac{\mathrm{2}}{\left(−{t}\right)}}=−\mathrm{2}\sqrt{\mathrm{2}}={local}\:{max} \\ $$
Commented by rahul 19 last updated on 30/Mar/19
thank you sir!
Commented by rahul 19 last updated on 30/Mar/19
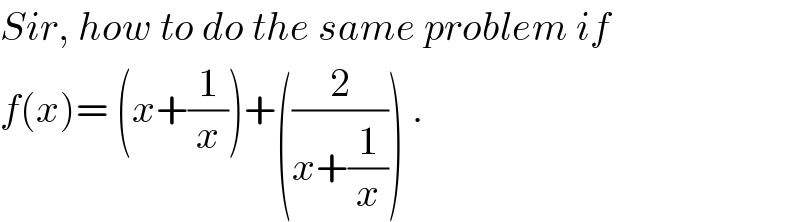
$${Sir},\:{how}\:{to}\:{do}\:{the}\:{same}\:{problem}\:{if}\: \\ $$$${f}\left({x}\right)=\:\left({x}+\frac{\mathrm{1}}{{x}}\right)+\left(\frac{\mathrm{2}}{{x}+\frac{\mathrm{1}}{{x}}}\right)\:. \\ $$
Commented by mr W last updated on 31/Mar/19
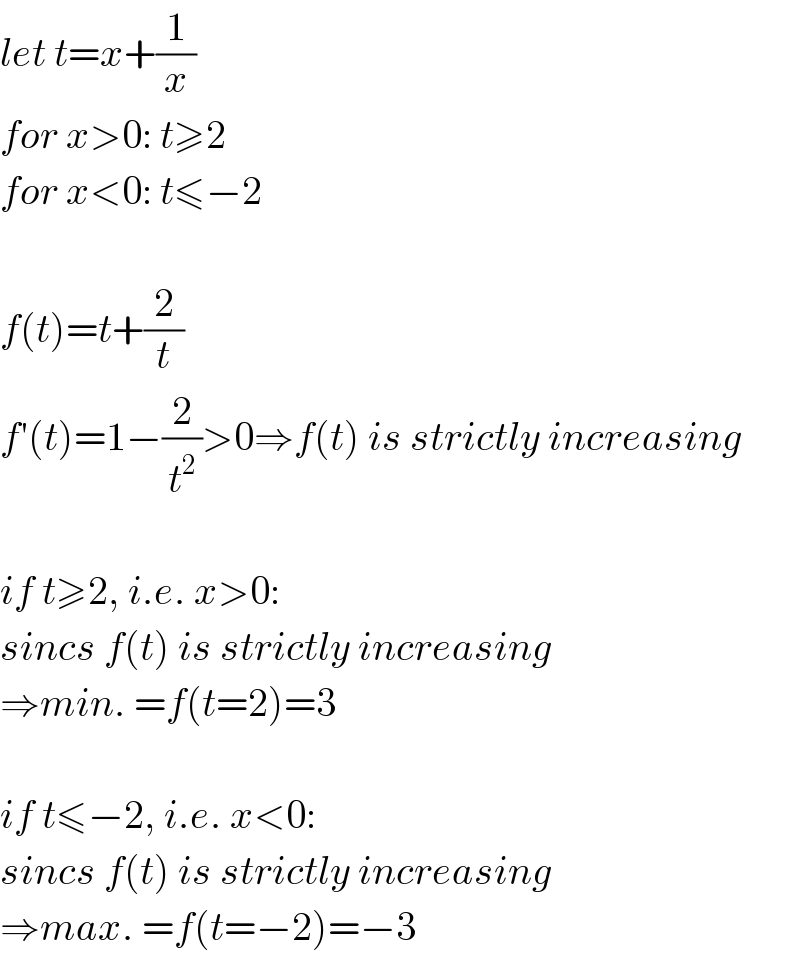
$${let}\:{t}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${for}\:{x}>\mathrm{0}:\:{t}\geqslant\mathrm{2} \\ $$$${for}\:{x}<\mathrm{0}:\:{t}\leqslant−\mathrm{2} \\ $$$$ \\ $$$${f}\left({t}\right)={t}+\frac{\mathrm{2}}{{t}} \\ $$$${f}'\left({t}\right)=\mathrm{1}−\frac{\mathrm{2}}{{t}^{\mathrm{2}} }>\mathrm{0}\Rightarrow{f}\left({t}\right)\:{is}\:{strictly}\:{increasing} \\ $$$$ \\ $$$${if}\:{t}\geqslant\mathrm{2},\:{i}.{e}.\:{x}>\mathrm{0}: \\ $$$${sincs}\:{f}\left({t}\right)\:{is}\:{strictly}\:{increasing} \\ $$$$\Rightarrow{min}.\:={f}\left({t}=\mathrm{2}\right)=\mathrm{3}\: \\ $$$$ \\ $$$${if}\:{t}\leqslant−\mathrm{2},\:{i}.{e}.\:{x}<\mathrm{0}: \\ $$$${sincs}\:{f}\left({t}\right)\:{is}\:{strictly}\:{increasing} \\ $$$$\Rightarrow{max}.\:={f}\left({t}=−\mathrm{2}\right)=−\mathrm{3}\: \\ $$
Commented by rahul 19 last updated on 31/Mar/19
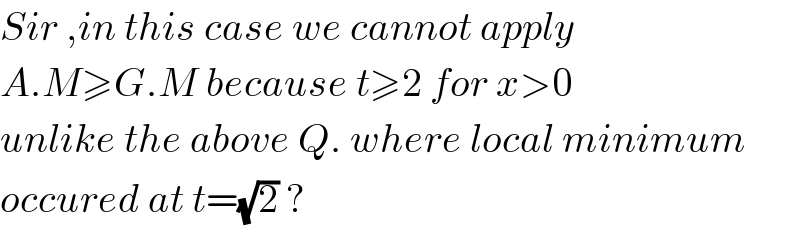
$${Sir}\:,{in}\:{this}\:{case}\:{we}\:{cannot}\:{apply} \\ $$$${A}.{M}\geqslant{G}.{M}\:{because}\:{t}\geqslant\mathrm{2}\:{for}\:{x}>\mathrm{0} \\ $$$${unlike}\:{the}\:{above}\:{Q}.\:{where}\:{local}\:{minimum} \\ $$$${occured}\:{at}\:{t}=\sqrt{\mathrm{2}}\:? \\ $$
Commented by mr W last updated on 31/Mar/19
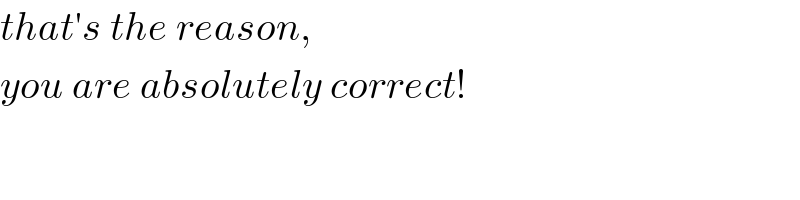
$${that}'{s}\:{the}\:{reason}, \\ $$$${you}\:{are}\:{absolutely}\:{correct}! \\ $$
Answered by MJS last updated on 28/Mar/19
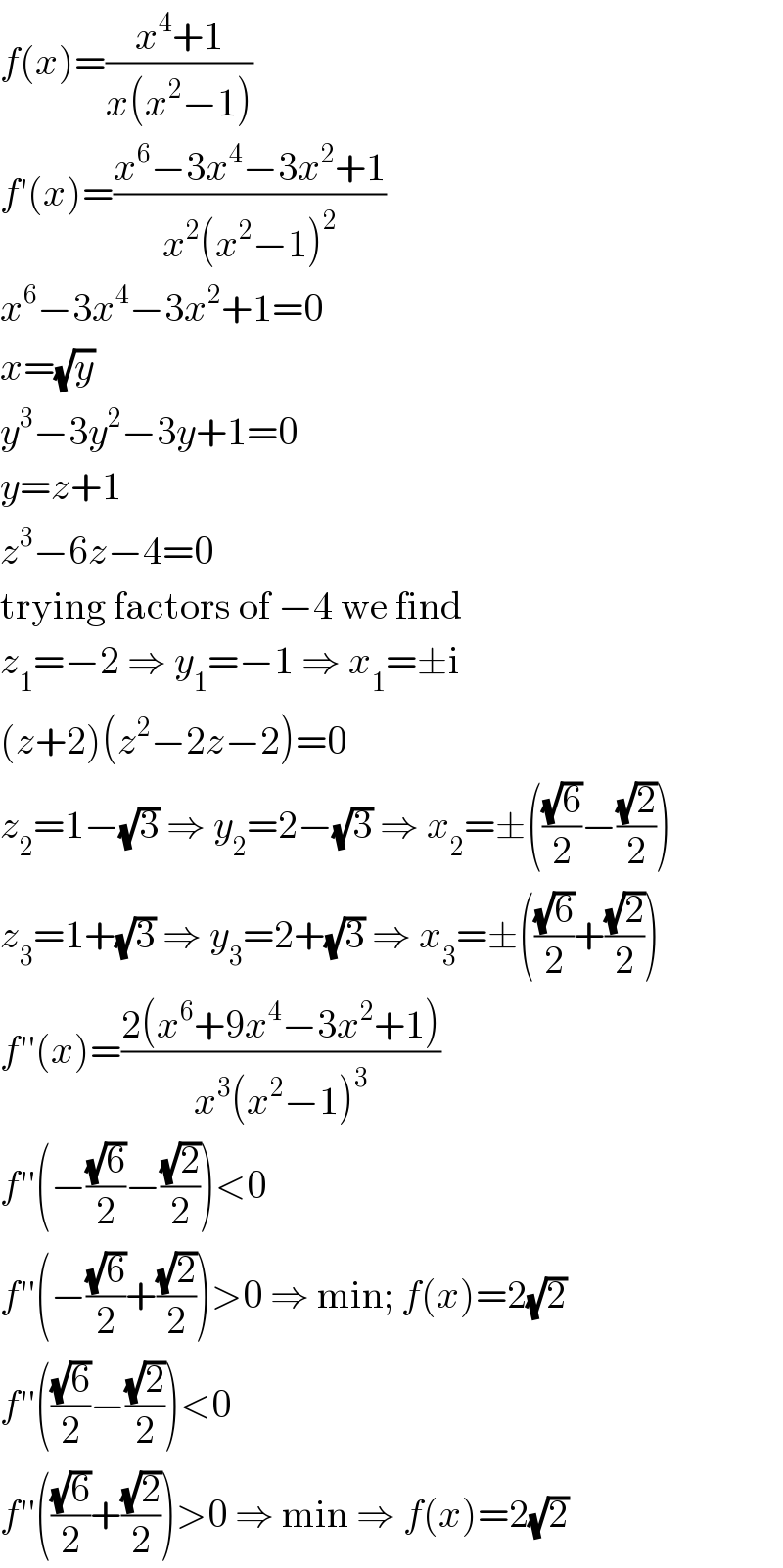
$${f}\left({x}\right)=\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$${f}'\left({x}\right)=\frac{{x}^{\mathrm{6}} −\mathrm{3}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${x}^{\mathrm{6}} −\mathrm{3}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}=\sqrt{{y}} \\ $$$${y}^{\mathrm{3}} −\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{1}=\mathrm{0} \\ $$$${y}={z}+\mathrm{1} \\ $$$${z}^{\mathrm{3}} −\mathrm{6}{z}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:−\mathrm{4}\:\mathrm{we}\:\mathrm{find} \\ $$$${z}_{\mathrm{1}} =−\mathrm{2}\:\Rightarrow\:{y}_{\mathrm{1}} =−\mathrm{1}\:\Rightarrow\:{x}_{\mathrm{1}} =\pm\mathrm{i} \\ $$$$\left({z}+\mathrm{2}\right)\left({z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{2}\right)=\mathrm{0} \\ $$$${z}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{3}}\:\Rightarrow\:{y}_{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{3}}\:\Rightarrow\:{x}_{\mathrm{2}} =\pm\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$${z}_{\mathrm{3}} =\mathrm{1}+\sqrt{\mathrm{3}}\:\Rightarrow\:{y}_{\mathrm{3}} =\mathrm{2}+\sqrt{\mathrm{3}}\:\Rightarrow\:{x}_{\mathrm{3}} =\pm\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$${f}''\left({x}\right)=\frac{\mathrm{2}\left({x}^{\mathrm{6}} +\mathrm{9}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${f}''\left(−\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)<\mathrm{0} \\ $$$${f}''\left(−\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)>\mathrm{0}\:\Rightarrow\:\mathrm{min};\:{f}\left({x}\right)=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${f}''\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)<\mathrm{0} \\ $$$${f}''\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)>\mathrm{0}\:\Rightarrow\:\mathrm{min}\:\Rightarrow\:{f}\left({x}\right)=\mathrm{2}\sqrt{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 30/Mar/19
thank you sir!
