
Previous in Relation and Functions Next in Relation and Functions
Question Number 57010 by 121194 last updated on 28/Mar/19
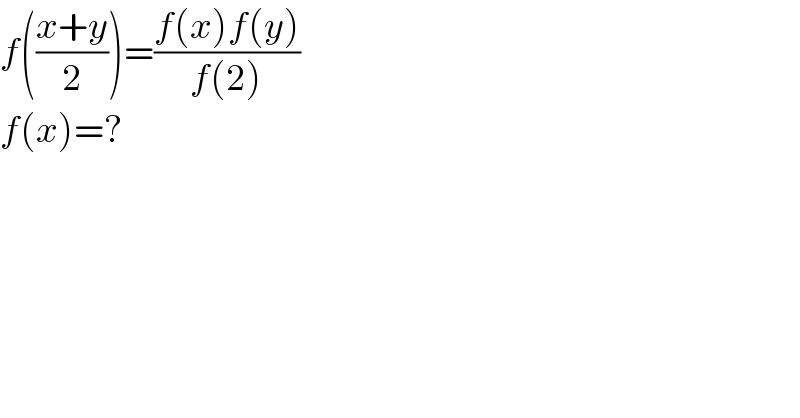
$${f}\left(\frac{{x}+{y}}{\mathrm{2}}\right)=\frac{{f}\left({x}\right){f}\left({y}\right)}{{f}\left(\mathrm{2}\right)} \\ $$$${f}\left({x}\right)=? \\ $$
Commented by maxmathsup by imad last updated on 29/Mar/19
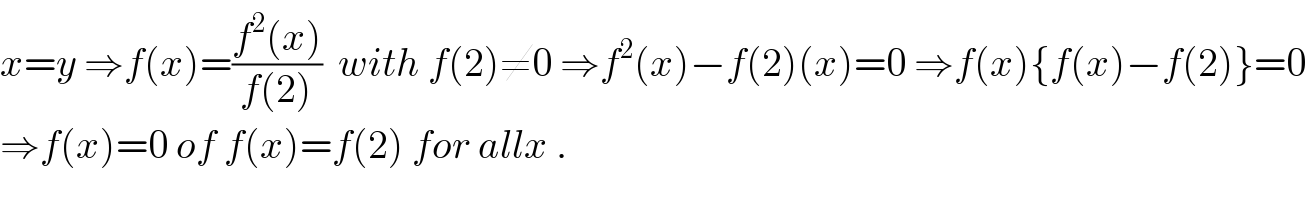
$${x}={y}\:\Rightarrow{f}\left({x}\right)=\frac{{f}^{\mathrm{2}} \left({x}\right)}{{f}\left(\mathrm{2}\right)}\:\:{with}\:{f}\left(\mathrm{2}\right)\neq\mathrm{0}\:\Rightarrow{f}^{\mathrm{2}} \left({x}\right)−{f}\left(\mathrm{2}\right)\left({x}\right)=\mathrm{0}\:\Rightarrow{f}\left({x}\right)\left\{{f}\left({x}\right)−{f}\left(\mathrm{2}\right)\right\}=\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{0}\:{of}\:{f}\left({x}\right)={f}\left(\mathrm{2}\right)\:{for}\:{allx}\:. \\ $$
Answered by kaivan.ahmadi last updated on 28/Mar/19
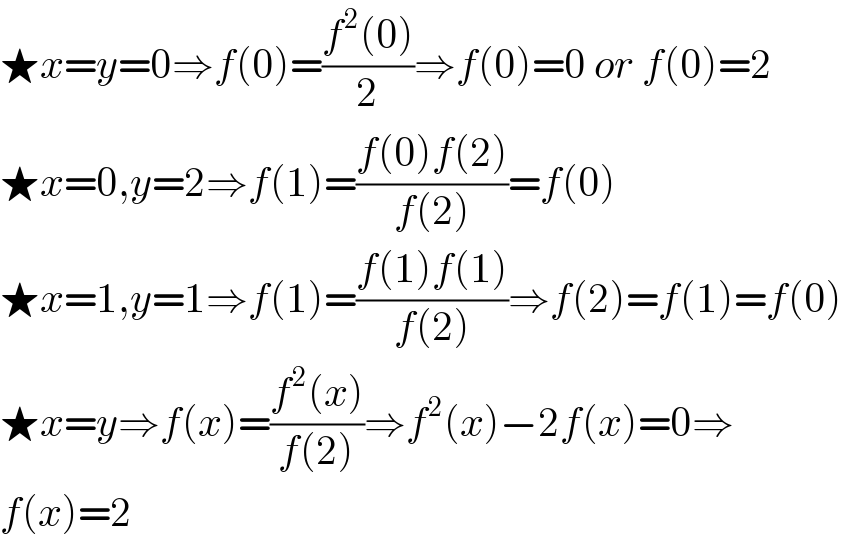
$$\bigstar{x}={y}=\mathrm{0}\Rightarrow{f}\left(\mathrm{0}\right)=\frac{{f}^{\mathrm{2}} \left(\mathrm{0}\right)}{\mathrm{2}}\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{0}\:{or}\:{f}\left(\mathrm{0}\right)=\mathrm{2} \\ $$$$\bigstar{x}=\mathrm{0},{y}=\mathrm{2}\Rightarrow{f}\left(\mathrm{1}\right)=\frac{{f}\left(\mathrm{0}\right){f}\left(\mathrm{2}\right)}{{f}\left(\mathrm{2}\right)}={f}\left(\mathrm{0}\right) \\ $$$$\bigstar{x}=\mathrm{1},{y}=\mathrm{1}\Rightarrow{f}\left(\mathrm{1}\right)=\frac{{f}\left(\mathrm{1}\right){f}\left(\mathrm{1}\right)}{{f}\left(\mathrm{2}\right)}\Rightarrow{f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}\right)={f}\left(\mathrm{0}\right) \\ $$$$\bigstar{x}={y}\Rightarrow{f}\left({x}\right)=\frac{{f}^{\mathrm{2}} \left({x}\right)}{{f}\left(\mathrm{2}\right)}\Rightarrow{f}^{\mathrm{2}} \left({x}\right)−\mathrm{2}{f}\left({x}\right)=\mathrm{0}\Rightarrow \\ $$$${f}\left({x}\right)=\mathrm{2} \\ $$
