
Question Number 56775 by zambolly19 last updated on 23/Mar/19
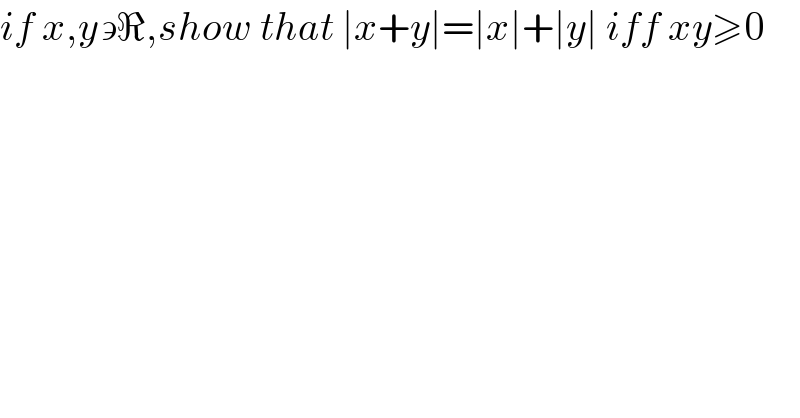
$${if}\:{x},{y}\backepsilon\Re,{show}\:{that}\:\mid{x}+{y}\mid=\mid{x}\mid+\mid{y}\mid\:{iff}\:{xy}\geqslant\mathrm{0} \\ $$
Commented by maxmathsup by imad last updated on 23/Mar/19
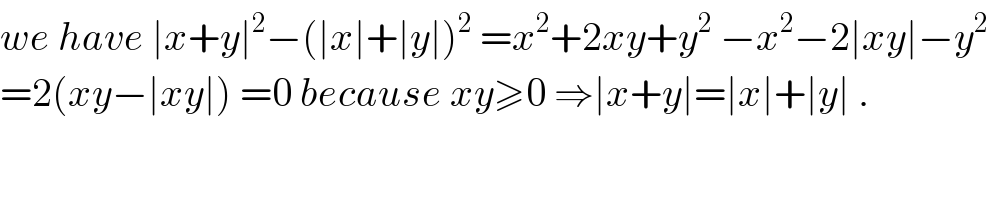
$${we}\:{have}\:\mid{x}+{y}\mid^{\mathrm{2}} −\left(\mid{x}\mid+\mid{y}\mid\right)^{\mathrm{2}} \:={x}^{\mathrm{2}} +\mathrm{2}{xy}+{y}^{\mathrm{2}} \:−{x}^{\mathrm{2}} −\mathrm{2}\mid{xy}\mid−{y}^{\mathrm{2}} \\ $$$$=\mathrm{2}\left({xy}−\mid{xy}\mid\right)\:=\mathrm{0}\:{because}\:{xy}\geqslant\mathrm{0}\:\Rightarrow\mid{x}+{y}\mid=\mid{x}\mid+\mid{y}\mid\:. \\ $$
