
Question Number 55415 by Tawa1 last updated on 23/Feb/19
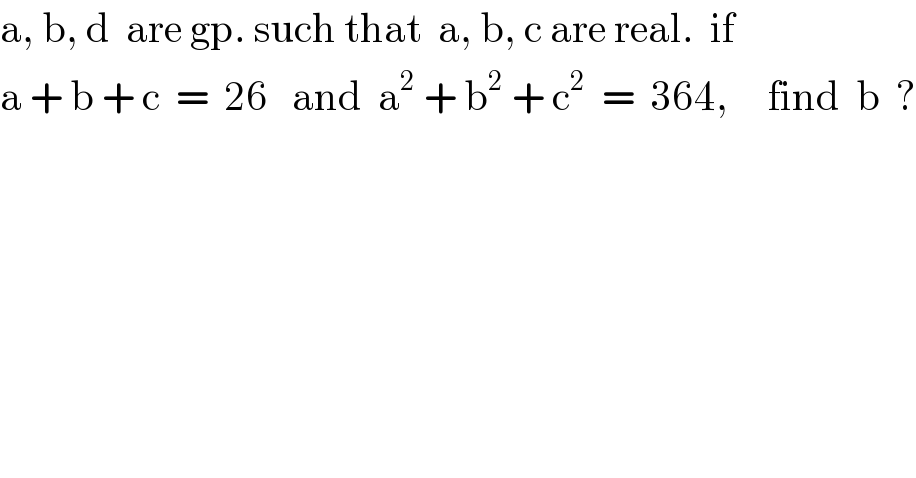
$$\mathrm{a},\:\mathrm{b},\:\mathrm{d}\:\:\mathrm{are}\:\mathrm{gp}.\:\mathrm{such}\:\mathrm{that}\:\:\mathrm{a},\:\mathrm{b},\:\mathrm{c}\:\mathrm{are}\:\mathrm{real}.\:\:\mathrm{if}\:\: \\ $$$$\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:\:=\:\:\mathrm{26}\:\:\:\mathrm{and}\:\:\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \:+\:\mathrm{c}^{\mathrm{2}} \:\:=\:\:\mathrm{364},\:\:\:\:\:\mathrm{find}\:\:\mathrm{b}\:\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Feb/19
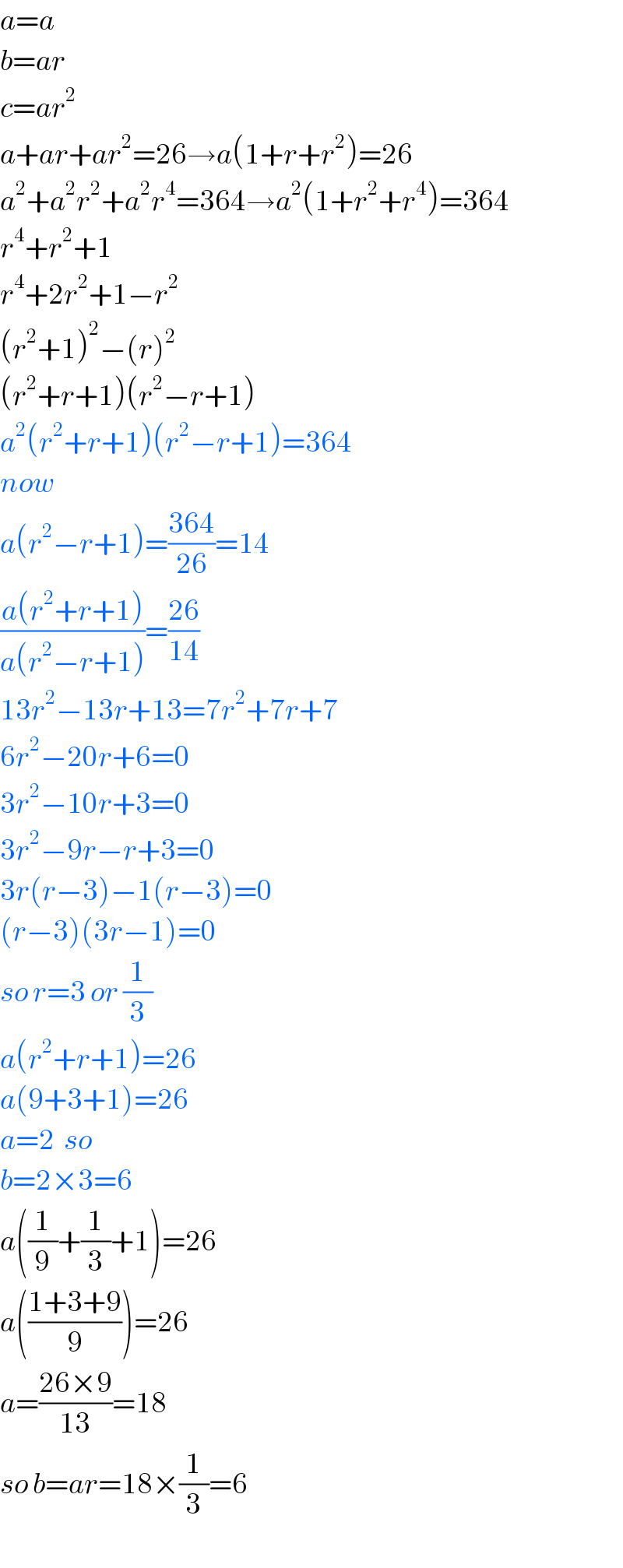
$${a}={a} \\ $$$${b}={ar} \\ $$$${c}={ar}^{\mathrm{2}} \\ $$$${a}+{ar}+{ar}^{\mathrm{2}} =\mathrm{26}\rightarrow{a}\left(\mathrm{1}+{r}+{r}^{\mathrm{2}} \right)=\mathrm{26} \\ $$$${a}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} +{a}^{\mathrm{2}} {r}^{\mathrm{4}} =\mathrm{364}\rightarrow{a}^{\mathrm{2}} \left(\mathrm{1}+{r}^{\mathrm{2}} +{r}^{\mathrm{4}} \right)=\mathrm{364} \\ $$$${r}^{\mathrm{4}} +{r}^{\mathrm{2}} +\mathrm{1} \\ $$$${r}^{\mathrm{4}} +\mathrm{2}{r}^{\mathrm{2}} +\mathrm{1}−{r}^{\mathrm{2}} \\ $$$$\left({r}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\left({r}\right)^{\mathrm{2}} \\ $$$$\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)\left({r}^{\mathrm{2}} −{r}+\mathrm{1}\right) \\ $$$${a}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)\left({r}^{\mathrm{2}} −{r}+\mathrm{1}\right)=\mathrm{364} \\ $$$${now} \\ $$$${a}\left({r}^{\mathrm{2}} −{r}+\mathrm{1}\right)=\frac{\mathrm{364}}{\mathrm{26}}=\mathrm{14} \\ $$$$\frac{{a}\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)}{{a}\left({r}^{\mathrm{2}} −{r}+\mathrm{1}\right)}=\frac{\mathrm{26}}{\mathrm{14}} \\ $$$$\mathrm{13}{r}^{\mathrm{2}} −\mathrm{13}{r}+\mathrm{13}=\mathrm{7}{r}^{\mathrm{2}} +\mathrm{7}{r}+\mathrm{7} \\ $$$$\mathrm{6}{r}^{\mathrm{2}} −\mathrm{20}{r}+\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{3}{r}^{\mathrm{2}} −\mathrm{10}{r}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}{r}^{\mathrm{2}} −\mathrm{9}{r}−{r}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}{r}\left({r}−\mathrm{3}\right)−\mathrm{1}\left({r}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\left({r}−\mathrm{3}\right)\left(\mathrm{3}{r}−\mathrm{1}\right)=\mathrm{0} \\ $$$${so}\:{r}=\mathrm{3}\:{or}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${a}\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)=\mathrm{26} \\ $$$${a}\left(\mathrm{9}+\mathrm{3}+\mathrm{1}\right)=\mathrm{26} \\ $$$${a}=\mathrm{2}\:\:{so} \\ $$$${b}=\mathrm{2}×\mathrm{3}=\mathrm{6} \\ $$$${a}\left(\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right)=\mathrm{26} \\ $$$${a}\left(\frac{\mathrm{1}+\mathrm{3}+\mathrm{9}}{\mathrm{9}}\right)=\mathrm{26} \\ $$$${a}=\frac{\mathrm{26}×\mathrm{9}}{\mathrm{13}}=\mathrm{18} \\ $$$${so}\:{b}={ar}=\mathrm{18}×\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{6} \\ $$
Commented by Tawa1 last updated on 23/Feb/19
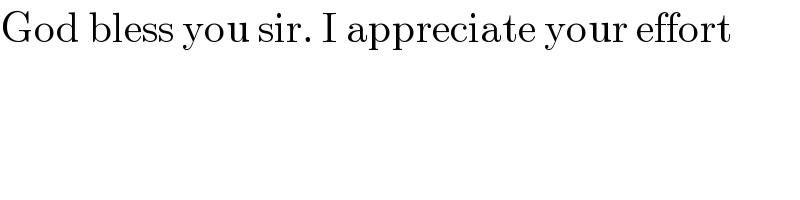
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort} \\ $$
Answered by peter frank last updated on 24/Feb/19
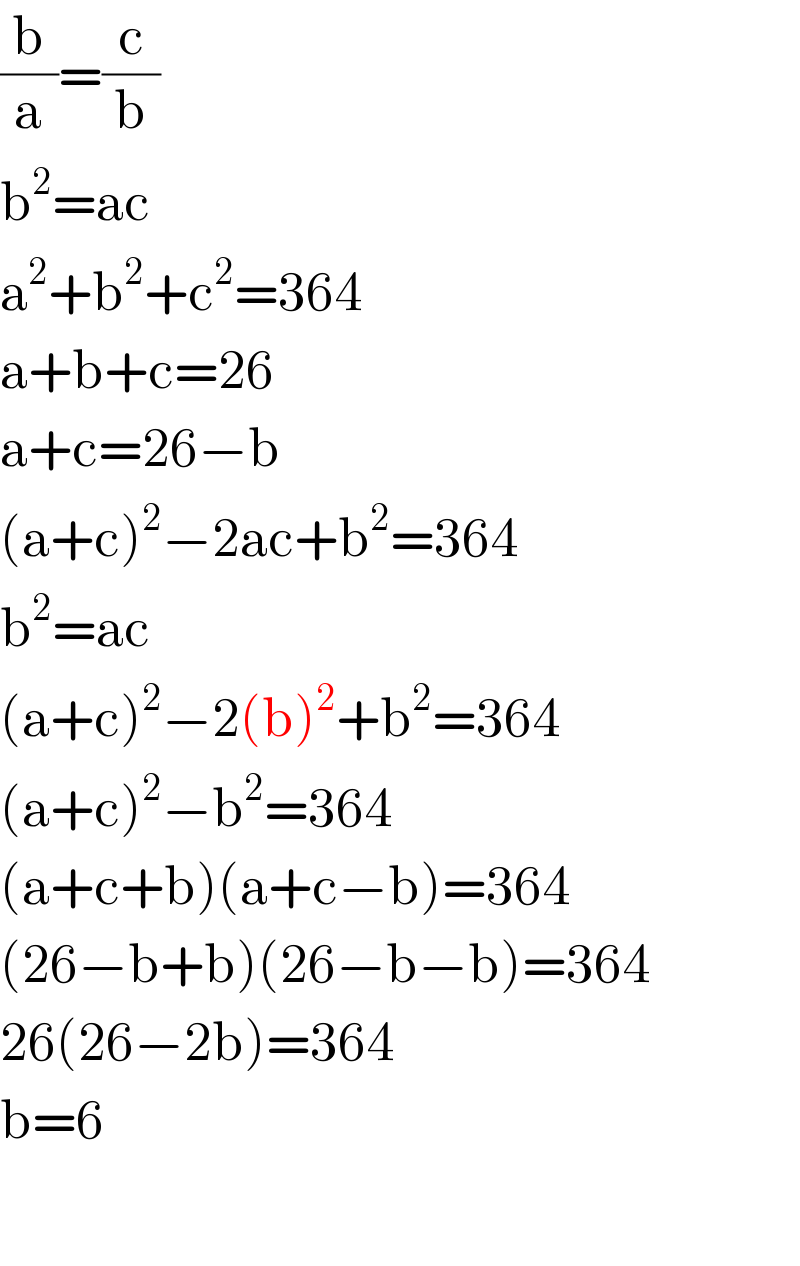
$$\frac{\mathrm{b}}{\mathrm{a}}=\frac{\mathrm{c}}{\mathrm{b}} \\ $$$$\mathrm{b}^{\mathrm{2}} =\mathrm{ac} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{364} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{26} \\ $$$$\mathrm{a}+\mathrm{c}=\mathrm{26}−\mathrm{b} \\ $$$$\left(\mathrm{a}+\mathrm{c}\right)^{\mathrm{2}} −\mathrm{2ac}+\mathrm{b}^{\mathrm{2}} =\mathrm{364} \\ $$$$\mathrm{b}^{\mathrm{2}} =\mathrm{ac} \\ $$$$\left(\mathrm{a}+\mathrm{c}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{b}\right)^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{364} \\ $$$$\left(\mathrm{a}+\mathrm{c}\right)^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =\mathrm{364} \\ $$$$\left(\mathrm{a}+\mathrm{c}+\mathrm{b}\right)\left(\mathrm{a}+\mathrm{c}−\mathrm{b}\right)=\mathrm{364} \\ $$$$\left(\mathrm{26}−\mathrm{b}+\mathrm{b}\right)\left(\mathrm{26}−\mathrm{b}−\mathrm{b}\right)=\mathrm{364} \\ $$$$\mathrm{26}\left(\mathrm{26}−\mathrm{2b}\right)=\mathrm{364} \\ $$$$\mathrm{b}=\mathrm{6} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 24/Feb/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
