
Question Number 54011 by maxmathsup by imad last updated on 27/Jan/19
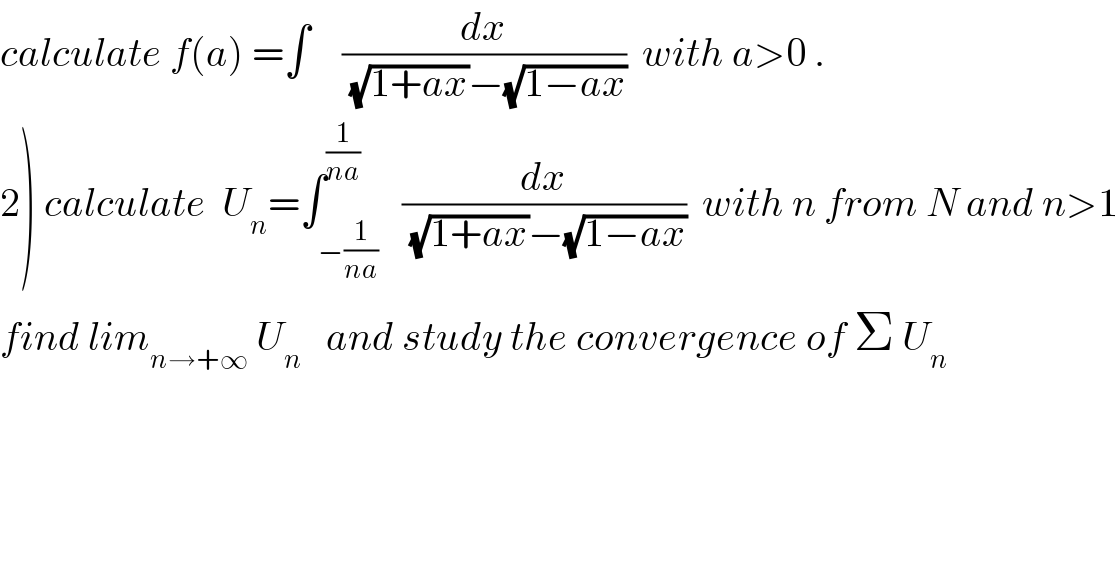
$${calculate}\:{f}\left({a}\right)\:=\int\:\:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{ax}}−\sqrt{\mathrm{1}−{ax}}}\:\:{with}\:{a}>\mathrm{0}\:. \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:\:{U}_{{n}} =\int_{−\frac{\mathrm{1}}{{na}}} ^{\frac{\mathrm{1}}{{na}}} \:\:\frac{{dx}}{\sqrt{\mathrm{1}+{ax}}−\sqrt{\mathrm{1}−{ax}}}\:\:{with}\:{n}\:{from}\:{N}\:{and}\:{n}>\mathrm{1} \\ $$ $${find}\:{lim}_{{n}\rightarrow+\infty} \:{U}_{{n}} \:\:\:{and}\:{study}\:{the}\:{convergence}\:{of}\:\Sigma\:{U}_{{n}} \\ $$
Commented bymaxmathsup by imad last updated on 28/Jan/19

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=_{{ax}\:={t}} \:\:\int\:\:\:\:\:\frac{{dt}}{{a}\left(\sqrt{\mathrm{1}+{t}}−\sqrt{\mathrm{1}−{t}}\right)}\:\:\Rightarrow \\ $$ $${af}\left({a}\right)\:=\int\:\:\frac{\sqrt{\mathrm{1}+{t}}+\sqrt{\mathrm{1}−{t}}}{\mathrm{2}{t}}\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\sqrt{\mathrm{1}+{t}}}{{t}}{dt}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\sqrt{\mathrm{1}−{t}}}{{t}}\:{dt}\:\Rightarrow \\ $$ $$\mathrm{2}{af}\left({a}\right)\:=\:\int\:\frac{\sqrt{\mathrm{1}+{t}}}{{t}}\:{dt}\:+\int\:\frac{\sqrt{\mathrm{1}−{t}}}{{t}}\:{dt}\:\:{but} \\ $$ $$\int\:\frac{\sqrt{\mathrm{1}+{t}}}{{t}}{dt}\:\:=_{\mathrm{1}+{t}={u}^{\mathrm{2}} } \:\:\:\:\int\:\:\:\frac{{u}}{{u}^{\mathrm{2}} −\mathrm{1}}\:\left(\mathrm{2}{u}\right){du}\:=\mathrm{2}\:\int\:\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} −\mathrm{1}}\:{du} \\ $$ $$=\mathrm{2}\:\int\:\:\frac{{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{2}{u}\:+\mathrm{2}\:\int\:\:\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{2}{u}\:\:+\:\int\:\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$ $$=\mathrm{2}{u}\:+{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\:+{c}_{\mathrm{0}} \:\:=\mathrm{2}\sqrt{\mathrm{1}+{t}}+{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+{t}}}{\mathrm{1}−\sqrt{\mathrm{1}−{t}}}\mid\:+{c}_{\mathrm{0}} \\ $$ $$=\mathrm{2}\:\sqrt{\mathrm{1}+{ax}}\:+{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+{ax}}}{\mathrm{1}−\sqrt{\mathrm{1}−{ax}}}\mid\:\:+{c}_{\mathrm{0}} \:\:\:{also}\:{we}\:{have}\: \\ $$ $$\int\:\frac{\sqrt{\mathrm{1}−{t}}}{{t}}\:{dt}\:=_{\mathrm{1}−{t}\:={u}^{\mathrm{2}} } \:\:\:\:\int\:\:\frac{{u}}{\mathrm{1}−{u}^{\mathrm{2}} }\:\left(−\mathrm{2}{u}\right){du}\:=\:\mathrm{2}\:\int\:\:\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} \:−\mathrm{1}}\:\Rightarrow \\ $$ $$\mathrm{2}{af}\left({a}\right)\:=\mathrm{2}\:\int\:\frac{\sqrt{\mathrm{1}+{t}}}{{t}}\:{dt}\:\Rightarrow{f}\left({a}\right)\:=\frac{\mathrm{1}}{{a}}\left\{\mathrm{2}\sqrt{\mathrm{1}+{ax}}\:+{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+{ax}}}{\mathrm{1}−\sqrt{\mathrm{1}−{ax}}}\mid\right\}\:. \\ $$ $${f}\left({a}\right)\:=\frac{\mathrm{1}}{{a}}\left\{\mathrm{2}\sqrt{\mathrm{1}+{ax}}+{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+{ax}}}{\mathrm{1}−\sqrt{\mathrm{1}−{ax}}}\mid\right\}\:+{C}\:. \\ $$
Commented bymaxmathsup by imad last updated on 28/Jan/19
![2) we have U_n =∫_(−(1/(na))) ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) =2lim_(ξ→0) ∫_ξ ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) but ∫_ξ ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) =[(1/a)(2(√(1+ax))+ln∣((1+(√(1+ax)))/(1−(√(1−ax))))∣)]_(x=ξ) ^(1/(na)) =(1/a){2(√(1+(1/n)))+ln∣((1+(√(1+(1/n))))/(1−(√(1−(1/n)))))∣−2(√(1+aξ))−ln∣((1+(√(1+aξ)))/(1−(√(1−aξ))))∣} but we cant find lim U_n from this quantity be continued...](Q54063.png)
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{U}_{{n}} =\int_{−\frac{\mathrm{1}}{{na}}} ^{\frac{\mathrm{1}}{{na}}} \:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{ax}}−\sqrt{\mathrm{1}−{ax}}}\:=\mathrm{2}{lim}_{\xi\rightarrow\mathrm{0}} \:\int_{\xi} ^{\frac{\mathrm{1}}{{na}}} \:\:\frac{{dx}}{\sqrt{\mathrm{1}+{ax}}−\sqrt{\mathrm{1}−{ax}}} \\ $$ $${but}\:\int_{\xi} ^{\frac{\mathrm{1}}{{na}}} \:\:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{ax}}−\sqrt{\mathrm{1}−{ax}}}\:=\left[\frac{\mathrm{1}}{{a}}\left(\mathrm{2}\sqrt{\mathrm{1}+{ax}}+{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+{ax}}}{\mathrm{1}−\sqrt{\mathrm{1}−{ax}}}\mid\right)\right]_{{x}=\xi} ^{\frac{\mathrm{1}}{{na}}} \\ $$ $$=\frac{\mathrm{1}}{{a}}\left\{\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}}}+{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}}}}{\mathrm{1}−\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{n}}}}\mid−\mathrm{2}\sqrt{\mathrm{1}+{a}\xi}−{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+{a}\xi}}{\mathrm{1}−\sqrt{\mathrm{1}−{a}\xi}}\mid\right\} \\ $$ $${but}\:{we}\:{cant}\:{find}\:{lim}\:{U}_{{n}} \:{from}\:{this}\:{quantity}\:\:{be}\:{continued}... \\ $$ $$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jan/19
![∫(((√(1+ax)) +(√(1−ax)))/(2ax))dx ∫((√(1+ax))/(2ax))dx+∫((√(1−ax))/(2ax))dx t_1 ^2 =1+ax 2t_1 dt=adx t_2 ^2 =1−ax 2t_2 dt=−adx ∫((t_1 ×2t_1 dt)/(2a(t_1 ^2 −1)))+∫((t_2 ×−2t_2 )/(2a×(1−t_1 ^2 )))dt_2 (1/a)∫((t_1 ^2 −1+1)/(t_1 ^2 −1))dt_1 +(1/a)∫((1−t_2 ^2 −1)/(1−t_2 ^2 ))dt_2 (1/a)[∫dt_1 +∫(dt_1 /(t_2 ^2 −1))+∫dt_2 −∫(dt_2 /(1−t_2 ^2 ))] now use formula...](Q54018.png)
$$\int\frac{\sqrt{\mathrm{1}+{ax}}\:+\sqrt{\mathrm{1}−{ax}}}{\mathrm{2}{ax}}{dx} \\ $$ $$\int\frac{\sqrt{\mathrm{1}+{ax}}}{\mathrm{2}{ax}}{dx}+\int\frac{\sqrt{\mathrm{1}−{ax}}}{\mathrm{2}{ax}}{dx} \\ $$ $${t}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{1}+{ax}\:\:\:\mathrm{2}{t}_{\mathrm{1}} {dt}={adx} \\ $$ $${t}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{1}−{ax}\:\:\mathrm{2}{t}_{\mathrm{2}} {dt}=−{adx} \\ $$ $$\int\frac{{t}_{\mathrm{1}} ×\mathrm{2}{t}_{\mathrm{1}} {dt}}{\mathrm{2}{a}\left({t}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}\right)}+\int\frac{{t}_{\mathrm{2}} ×−\mathrm{2}{t}_{\mathrm{2}} }{\mathrm{2}{a}×\left(\mathrm{1}−{t}_{\mathrm{1}} ^{\mathrm{2}} \right)}{dt}_{\mathrm{2}} \\ $$ $$\frac{\mathrm{1}}{{a}}\int\frac{{t}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{t}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}{dt}_{\mathrm{1}} +\frac{\mathrm{1}}{{a}}\int\frac{\mathrm{1}−{t}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−{t}_{\mathrm{2}} ^{\mathrm{2}} }{dt}_{\mathrm{2}} \\ $$ $$\frac{\mathrm{1}}{{a}}\left[\int{dt}_{\mathrm{1}} +\int\frac{{dt}_{\mathrm{1}} }{{t}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}+\int{dt}_{\mathrm{2}} −\int\frac{{dt}_{\mathrm{2}} }{\mathrm{1}−{t}_{\mathrm{2}} ^{\mathrm{2}} }\right] \\ $$ $${now}\:{use}\:{formula}... \\ $$ $$ \\ $$
