
Question Number 53966 by maxmathsup by imad last updated on 27/Jan/19
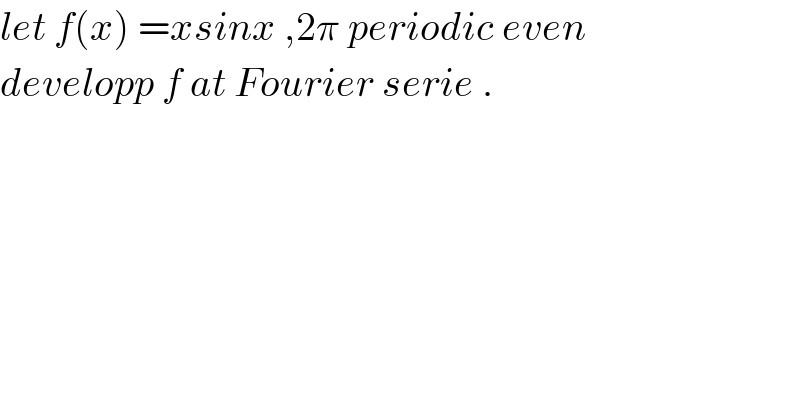
$${let}\:{f}\left({x}\right)\:={xsinx}\:,\mathrm{2}\pi\:{periodic}\:{even} \\ $$$${developp}\:{f}\:{at}\:{Fourier}\:{serie}\:. \\ $$
Commented by maxmathsup by imad last updated on 30/Jan/19
![f(x)=(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) and a_n =(2/T) ∫_([T]) f(x) cos(nx)dx =(2/(2π)) ∫_(−π) ^π xsin(x) cos(nx)dx =(2/π) ∫_0 ^π x sin(x)cos(nx) dx but sin(a+b) =sina cosb +cosa sinb sin(a−b)=sina cosb −cosa sinb ⇒sina cosb=(1/2){sin(a+b)+sin(a−b)} ⇒ (π/2) a_n =(1/2) ∫_0 ^π x{sin(n+1)x−sin(n−1)x}dx ⇒ π a_n =∫_0 ^π x sin(n+1)x dx −∫_0 ^π x sin(n−1)xdx let find I=∫_0 ^π x sin(αx)dx by parts I =[−(x/α)cos(αx)]_0 ^π −∫_0 ^π −(1/α) cos(αx)dx =−(1/α)[ xcos(αx)]_0 ^π +(1/α)[(1/α)sin(αx)]_0 ^π =−(π/α) cos(πα) +(1/α^2 ) sin(απ) ⇒ πa_n =−(π/(n+1))(−1)^(n+1) −(−(π/(n−1))(−1)^(n−1) ) =((π(−1)^n )/(n+1)) −((π(−1)^n )/(n−1)) =π(−1)^n {(1/(n+1)) −(1/(n−1))} =((−2π(−1)^n )/(n^2 −1)) =((2π(−1)^(n−1) )/(n^2 −1)) with n≥2 a_0 =(2/π) ∫_0 ^π xsin(x)dx =(2/π){π}=2 ⇒(a_0 /2) =1 (π/2) a_1 =∫_0 ^π xsin(2x)dx =−(π/2) ⇒a_1 =−1 ⇒ xsin(x) =2Σ_(n=2) ^∞ (((−1)^(n−1) )/(n^2 −1)) cos(nx).](Q54204.png)
$${f}\left({x}\right)=\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} {cos}\left({nx}\right)\:\:{and}\:{a}_{{n}} =\frac{\mathrm{2}}{{T}}\:\int_{\left[{T}\right]} \:\:{f}\left({x}\right)\:{cos}\left({nx}\right){dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}\pi}\:\int_{−\pi} ^{\pi} \:{xsin}\left({x}\right)\:{cos}\left({nx}\right){dx}\:=\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:{x}\:{sin}\left({x}\right){cos}\left({nx}\right)\:{dx}\:\:{but} \\ $$$${sin}\left({a}+{b}\right)\:={sina}\:{cosb}\:+{cosa}\:{sinb}\: \\ $$$${sin}\left({a}−{b}\right)={sina}\:{cosb}\:−{cosa}\:{sinb}\:\Rightarrow{sina}\:{cosb}=\frac{\mathrm{1}}{\mathrm{2}}\left\{{sin}\left({a}+{b}\right)+{sin}\left({a}−{b}\right)\right\}\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}\:{a}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\pi} \:{x}\left\{{sin}\left({n}+\mathrm{1}\right){x}−{sin}\left({n}−\mathrm{1}\right){x}\right\}{dx}\:\Rightarrow \\ $$$$\pi\:{a}_{{n}} =\int_{\mathrm{0}} ^{\pi} {x}\:{sin}\left({n}+\mathrm{1}\right){x}\:{dx}\:−\int_{\mathrm{0}} ^{\pi} \:{x}\:{sin}\left({n}−\mathrm{1}\right){xdx}\:{let}\:{find} \\ $$$${I}=\int_{\mathrm{0}} ^{\pi} \:{x}\:{sin}\left(\alpha{x}\right){dx}\:\:{by}\:{parts}\:{I}\:=\left[−\frac{{x}}{\alpha}{cos}\left(\alpha{x}\right)\right]_{\mathrm{0}} ^{\pi} \:−\int_{\mathrm{0}} ^{\pi} \:−\frac{\mathrm{1}}{\alpha}\:{cos}\left(\alpha{x}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\alpha}\left[\:{xcos}\left(\alpha{x}\right)\right]_{\mathrm{0}} ^{\pi} \:\:+\frac{\mathrm{1}}{\alpha}\left[\frac{\mathrm{1}}{\alpha}{sin}\left(\alpha{x}\right)\right]_{\mathrm{0}} ^{\pi} \:=−\frac{\pi}{\alpha}\:{cos}\left(\pi\alpha\right)\:+\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }\:{sin}\left(\alpha\pi\right)\:\Rightarrow \\ $$$$\pi{a}_{{n}} =−\frac{\pi}{{n}+\mathrm{1}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:−\left(−\frac{\pi}{{n}−\mathrm{1}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \right)\:=\frac{\pi\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:−\frac{\pi\left(−\mathrm{1}\right)^{{n}} }{{n}−\mathrm{1}} \\ $$$$=\pi\left(−\mathrm{1}\right)^{{n}} \left\{\frac{\mathrm{1}}{{n}+\mathrm{1}}\:−\frac{\mathrm{1}}{{n}−\mathrm{1}}\right\}\:=\frac{−\mathrm{2}\pi\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{2}\pi\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} −\mathrm{1}}\:\:{with}\:{n}\geqslant\mathrm{2} \\ $$$${a}_{\mathrm{0}} =\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:{xsin}\left({x}\right){dx}\:=\frac{\mathrm{2}}{\pi}\left\{\pi\right\}=\mathrm{2}\:\Rightarrow\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:=\mathrm{1} \\ $$$$\frac{\pi}{\mathrm{2}}\:{a}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\pi} \:{xsin}\left(\mathrm{2}{x}\right){dx}\:=−\frac{\pi}{\mathrm{2}}\:\Rightarrow{a}_{\mathrm{1}} =−\mathrm{1}\:\Rightarrow\: \\ $$$${xsin}\left({x}\right)\:=\mathrm{2}\sum_{{n}=\mathrm{2}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} −\mathrm{1}}\:{cos}\left({nx}\right). \\ $$
