
Question Number 53727 by Tawa1 last updated on 25/Jan/19

Answered by Kunal12588 last updated on 25/Jan/19
![just trying T_1 ,T_2 ,T_3 ,T_4 −lower cables T_1 =T_2 =T_3 =T_4 =k (identical cables) (1/2)((√(2^2 +0.5^2 )))=h tan^(−1) (2/h)=φ 4k cosφ−mg=0 4kcosφ=w k=((4.9)/(4cosφ)) T_(upper) =4kcosφ [not solved it bcuz i think its wrong] please report with answer](Q53766.png)
$${just}\:{trying} \\ $$$${T}_{\mathrm{1}} ,{T}_{\mathrm{2}} ,{T}_{\mathrm{3}} ,{T}_{\mathrm{4}} −{lower}\:{cables} \\ $$$${T}_{\mathrm{1}} ={T}_{\mathrm{2}} ={T}_{\mathrm{3}} ={T}_{\mathrm{4}} ={k}\:\:\:\:\:\:\:\left({identical}\:{cables}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{0}.\mathrm{5}^{\mathrm{2}} }\right)={h} \\ $$$${tan}^{−\mathrm{1}} \left(\mathrm{2}/{h}\right)=\phi \\ $$$$\mathrm{4}{k}\:{cos}\phi−{mg}=\mathrm{0} \\ $$$$\mathrm{4}{kcos}\phi={w} \\ $$$${k}=\frac{\mathrm{4}.\mathrm{9}}{\mathrm{4}{cos}\phi} \\ $$$${T}_{{upper}} =\mathrm{4}{kcos}\phi\:\:\:\:\:\:\left[{not}\:{solved}\:{it}\:{bcuz}\:{i}\:{think}\:{its}\:{wrong}\right] \\ $$$${please}\:{report}\:{with}\:{answer} \\ $$
Commented by Tawa1 last updated on 25/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19
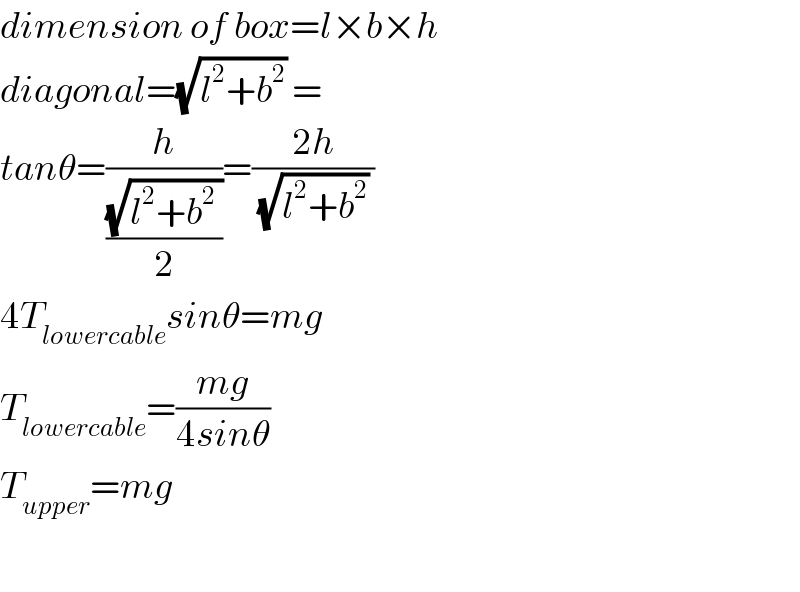
$${dimension}\:{of}\:{box}={l}×{b}×{h} \\ $$$${diagonal}=\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:= \\ $$$${tan}\theta=\frac{{h}}{\frac{\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} \:}}{\mathrm{2}}}=\frac{\mathrm{2}{h}}{\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:} \\ $$$$\mathrm{4}{T}_{{lowercable}} {sin}\theta={mg} \\ $$$${T}_{{lowercable}} =\frac{{mg}}{\mathrm{4}{sin}\theta} \\ $$$${T}_{{upper}} ={mg} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 25/Jan/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{you}\:\mathrm{can}\:\mathrm{help}\:\mathrm{me}\:\mathrm{complete}\:\mathrm{it}\:\mathrm{if}\:\mathrm{correct}\:\mathrm{sir}. \\ $$
