
Question Number 53647 by Tawa1 last updated on 24/Jan/19
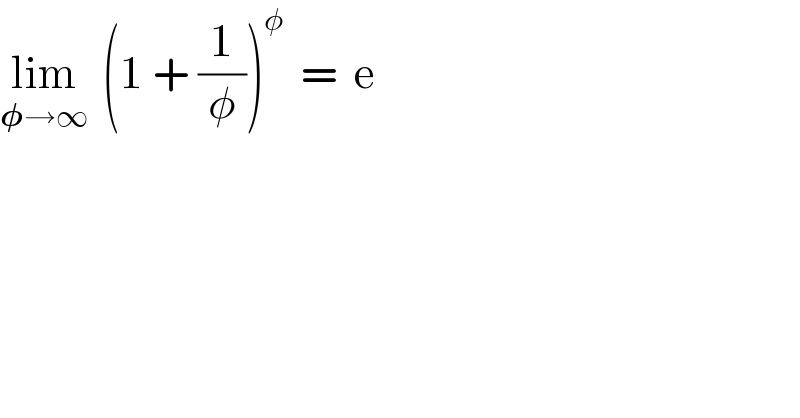
$$\underset{\boldsymbol{\phi}\rightarrow\infty} {\mathrm{lim}}\:\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\phi}\right)^{\phi} \:\:=\:\:\mathrm{e} \\ $$
Commented by maxmathsup by imad last updated on 24/Jan/19
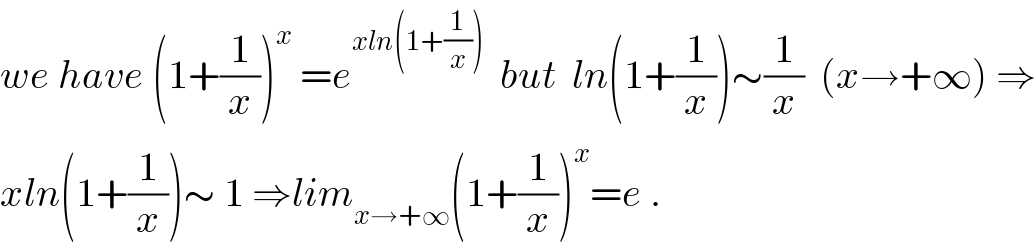
$${we}\:{have}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} \:={e}^{{xln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)} \:\:{but}\:\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\sim\frac{\mathrm{1}}{{x}}\:\:\left({x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${xln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\sim\:\mathrm{1}\:\Rightarrow{lim}_{{x}\rightarrow+\infty} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} ={e}\:. \\ $$
Commented by Tawa1 last updated on 24/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Jan/19
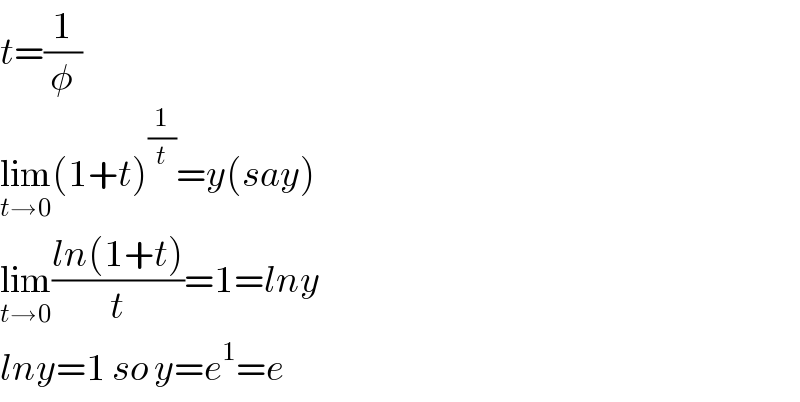
$${t}=\frac{\mathrm{1}}{\phi} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{1}}{{t}}} ={y}\left({say}\right) \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}=\mathrm{1}={lny} \\ $$$${lny}=\mathrm{1}\:{so}\:{y}={e}^{\mathrm{1}} ={e} \\ $$
Commented by Tawa1 last updated on 24/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
