Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 53532 by gunawan last updated on 23/Jan/19

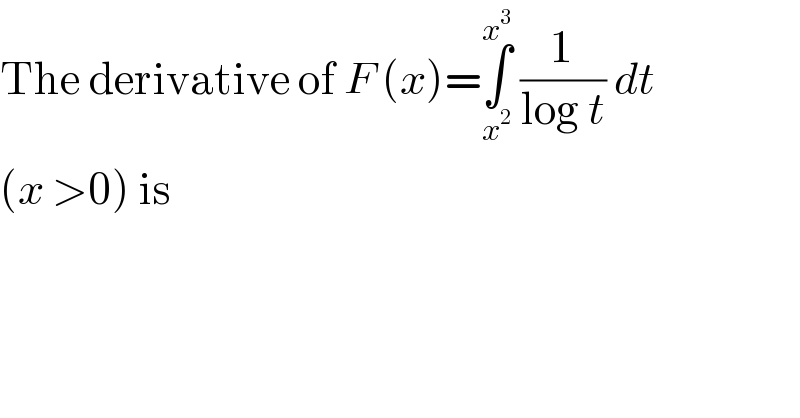
The derivative of F (x)=∫_x^2 ^x^3 (1/(log t)) dt (x >0) is

$$\mathrm{The}\:\mathrm{derivative}\:\mathrm{of}\:{F}\:\left({x}\right)=\underset{{x}^{\mathrm{2}} } {\overset{{x}^{\mathrm{3}} } {\int}}\:\frac{\mathrm{1}}{\mathrm{log}\:{t}}\:{dt} \\ $$ $$\left({x}\:>\mathrm{0}\right)\:\mathrm{is} \\ $$

Commented byAbdo msup. last updated on 23/Jan/19

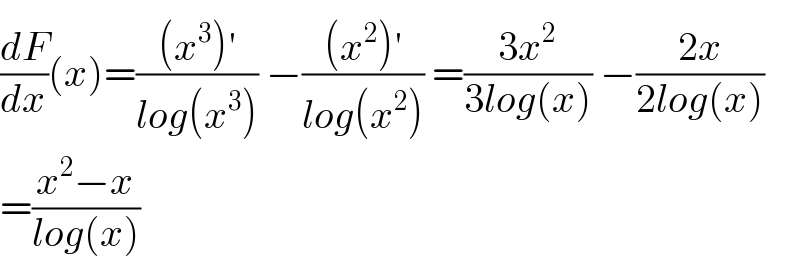
(dF/dx)(x)=(((x^3 )^′ )/(log(x^3 ))) −(((x^2 )^′ )/(log(x^2 ))) =((3x^2 )/(3log(x))) −((2x)/(2log(x))) =((x^2 −x)/(log(x)))

$$\frac{{dF}}{{dx}}\left({x}\right)=\frac{\left({x}^{\mathrm{3}} \right)^{'} }{{log}\left({x}^{\mathrm{3}} \right)}\:−\frac{\left({x}^{\mathrm{2}} \right)^{'} }{{log}\left({x}^{\mathrm{2}} \right)}\:=\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{3}{log}\left({x}\right)}\:−\frac{\mathrm{2}{x}}{\mathrm{2}{log}\left({x}\right)} \\ $$ $$=\frac{{x}^{\mathrm{2}} −{x}}{{log}\left({x}\right)} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jan/19

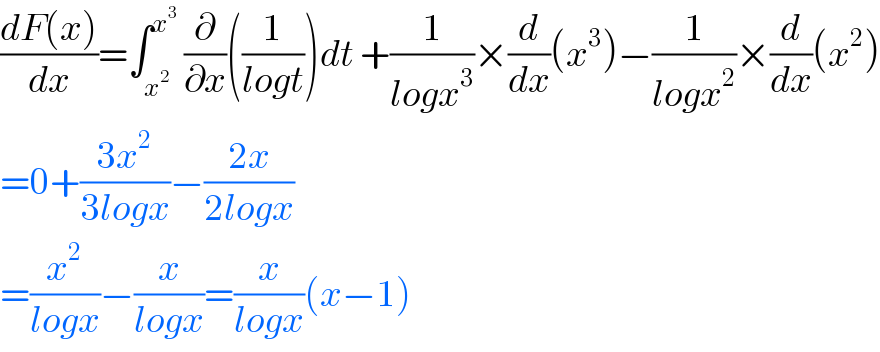
((dF(x))/dx)=∫_x^2 ^x^3 (∂/∂x)((1/(logt)))dt +(1/(logx^3 ))×(d/dx)(x^3 )−(1/(logx^2 ))×(d/dx)(x^2 ) =0+((3x^2 )/(3logx))−((2x)/(2logx)) =(x^2 /(logx))−(x/(logx))=(x/(logx))(x−1)

$$\frac{{dF}\left({x}\right)}{{dx}}=\int_{{x}^{\mathrm{2}} } ^{{x}^{\mathrm{3}} } \:\frac{\partial}{\partial{x}}\left(\frac{\mathrm{1}}{{logt}}\right){dt}\:+\frac{\mathrm{1}}{{logx}^{\mathrm{3}} }×\frac{{d}}{{dx}}\left({x}^{\mathrm{3}} \right)−\frac{\mathrm{1}}{{logx}^{\mathrm{2}} }×\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} \right) \\ $$ $$=\mathrm{0}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{3}{logx}}−\frac{\mathrm{2}{x}}{\mathrm{2}{logx}} \\ $$ $$=\frac{{x}^{\mathrm{2}} }{{logx}}−\frac{{x}}{{logx}}=\frac{{x}}{{logx}}\left({x}−\mathrm{1}\right) \\ $$

Commented bygunawan last updated on 23/Jan/19

thank you very much Sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$

Commented bymalwaan last updated on 23/Jan/19

0 how?

$$\mathrm{0}\:\:\mathrm{how}? \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 23/Jan/19

partial differentiation of F(t) w.r.t.x is x is 0

$${partial}\:{differentiation}\:{of}\:{F}\left({t}\right)\:{w}.{r}.{t}.{x}\:{is}\:{x}\:{is}\:\mathrm{0} \\ $$

Commented bymalwaan last updated on 24/Jan/19

Yes thank you so much sir

$$\mathrm{Yes} \\ $$ $$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com