
Question Number 53483 by dwdkswd last updated on 22/Jan/19
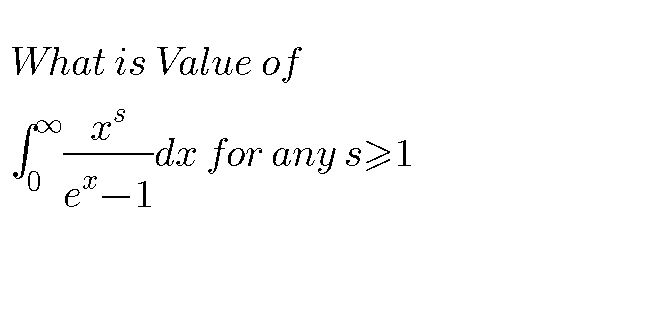
Commented by maxmathsup by imad last updated on 22/Jan/19
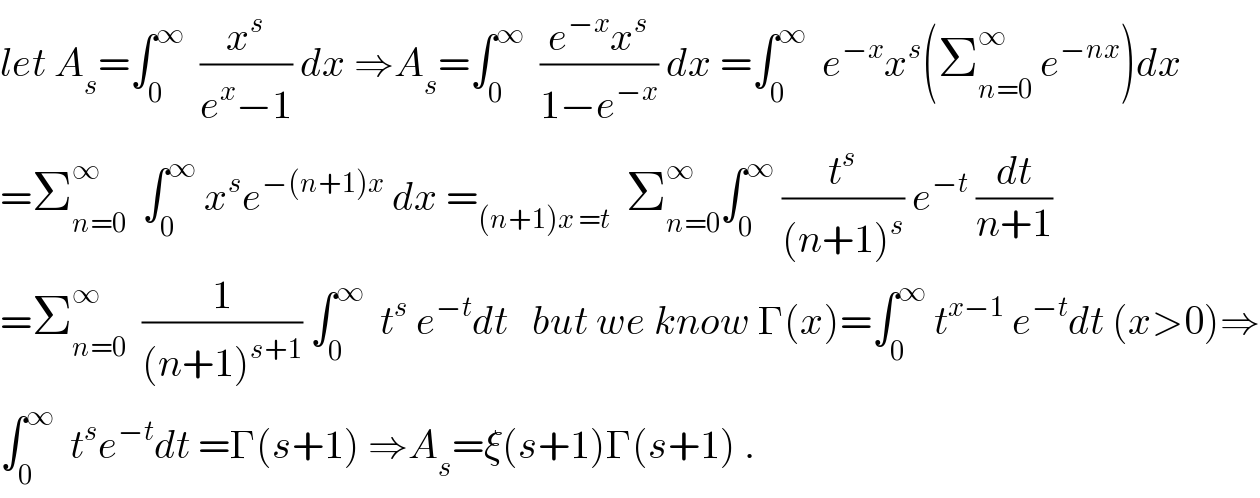
$${let}\:{A}_{{s}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{s}} }{{e}^{{x}} −\mathrm{1}}\:{dx}\:\Rightarrow{A}_{{s}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{x}} {x}^{{s}} }{\mathrm{1}−{e}^{−{x}} }\:{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}} {x}^{{s}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{nx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{\mathrm{0}} ^{\infty} \:{x}^{{s}} {e}^{−\left({n}+\mathrm{1}\right){x}} \:{dx}\:=_{\left({n}+\mathrm{1}\right){x}\:={t}} \:\:\sum_{{n}=\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{{s}} }{\left({n}+\mathrm{1}\right)^{{s}} }\:{e}^{−{t}} \:\frac{{dt}}{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{s}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\infty} \:\:{t}^{{s}} \:{e}^{−{t}} {dt}\:\:\:{but}\:{we}\:{know}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} {dt}\:\left({x}>\mathrm{0}\right)\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{t}^{{s}} {e}^{−{t}} {dt}\:=\Gamma\left({s}+\mathrm{1}\right)\:\Rightarrow{A}_{{s}} =\xi\left({s}+\mathrm{1}\right)\Gamma\left({s}+\mathrm{1}\right)\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19

Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19

Commented by Tawa1 last updated on 22/Jan/19
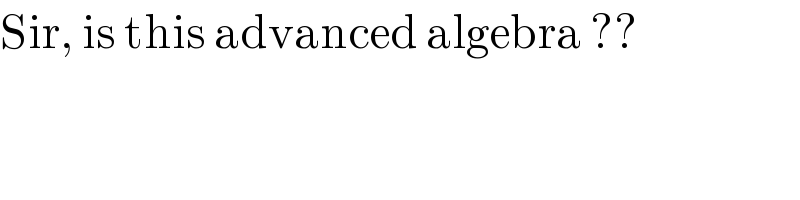
$$\mathrm{Sir},\:\mathrm{is}\:\mathrm{this}\:\mathrm{advanced}\:\mathrm{algebra}\:?? \\ $$
Commented by Tawa1 last updated on 22/Jan/19

$$\mathrm{I}\:\mathrm{mean}\:\mathrm{the}\:\mathrm{textbook}\:\mathrm{you}\:\mathrm{snaped} \\ $$
Commented by Tawa1 last updated on 22/Jan/19
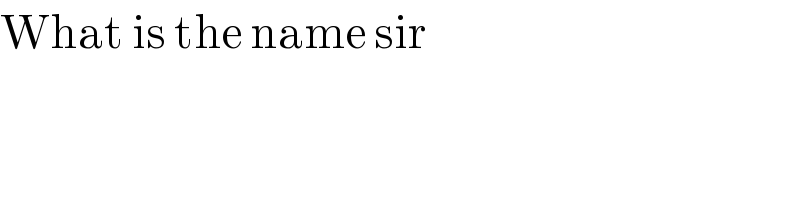
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{name}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19

Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
$${visit}\:{archive}.{org}\:{and}\:{free}\:{download}\:{it}..{the}\:{book} \\ $$
Commented by Tawa1 last updated on 22/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
