
Question Number 53386 by gunawan last updated on 21/Jan/19
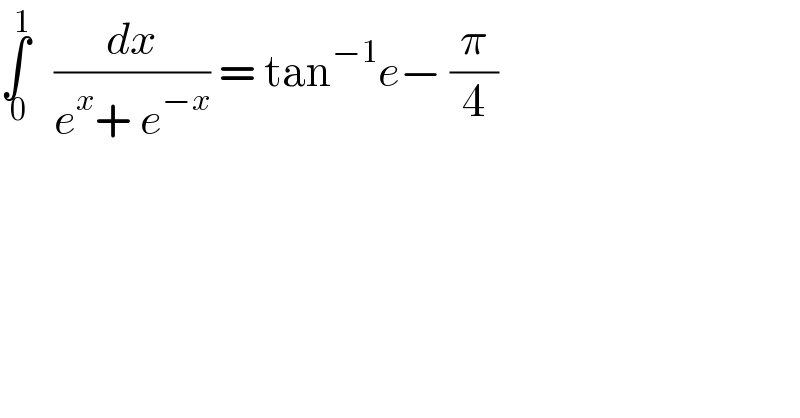
$$\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\:\frac{{dx}}{{e}^{{x}} +\:{e}^{−{x}} }\:=\:\mathrm{tan}^{−\mathrm{1}} {e}−\:\frac{\pi}{\mathrm{4}} \\ $$
Commented by Tinkutara last updated on 21/Jan/19
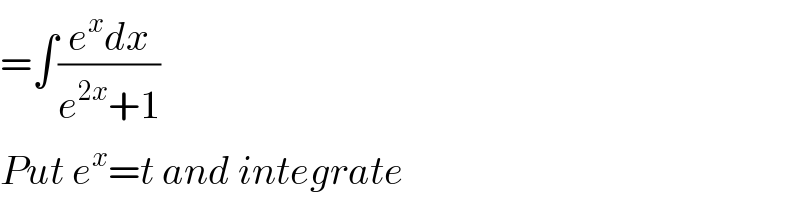
$$=\int\frac{{e}^{{x}} {dx}}{{e}^{\mathrm{2}{x}} +\mathrm{1}} \\ $$$${Put}\:{e}^{{x}} ={t}\:{and}\:{integrate} \\ $$
Commented by ajfour last updated on 21/Jan/19
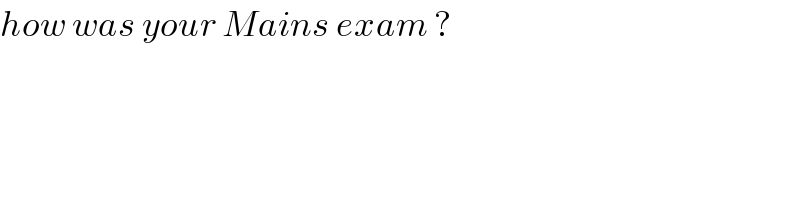
$${how}\:{was}\:{your}\:{Mains}\:{exam}\:? \\ $$
Commented by gunawan last updated on 21/Jan/19
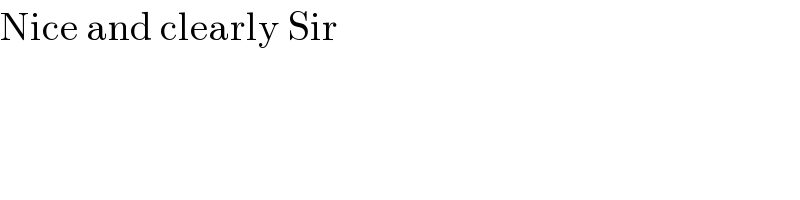
$$\mathrm{Nice}\:\mathrm{and}\:\mathrm{clearly}\:\mathrm{Sir} \\ $$
Commented by maxmathsup by imad last updated on 21/Jan/19
![let I =∫_0 ^1 (dx/(e^x +e^(−x) )) ⇒I=_(e^x =t) ∫_1 ^e (1/(t +t^(−1) )) (dt/t) =∫_1 ^e (dt/(t^2 +1)) =[arctan(t)]_1 ^e =arctan(e)−arctan(1)=arctan(e)−(π/4) .](Q53413.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{e}^{{x}} +{e}^{−{x}} }\:\Rightarrow{I}=_{{e}^{{x}} ={t}} \:\:\:\:\:\int_{\mathrm{1}} ^{{e}} \:\:\:\frac{\mathrm{1}}{{t}\:+{t}^{−\mathrm{1}} }\:\frac{{dt}}{{t}}\:=\int_{\mathrm{1}} ^{{e}} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\left[{arctan}\left({t}\right)\right]_{\mathrm{1}} ^{{e}} ={arctan}\left({e}\right)−{arctan}\left(\mathrm{1}\right)={arctan}\left({e}\right)−\frac{\pi}{\mathrm{4}}\:. \\ $$
Commented by Tinkutara last updated on 24/Jan/19
@ajfour Sir My Mains went well above my nervous expectations… I topped in my district Thanks for your continuous support sir And thanks to this wonderful platform… ��
Commented by ajfour last updated on 24/Jan/19

$${Its}\:{all}\:{a}\:{matter}\:{of}\:{your}\:{curiosity}\: \\ $$$${and}\:{willingness}\:{to}\:{learn}.\:{I}\:{too}, \\ $$$${had}\:{enjoyed}\:{solving}\:{your}\:{doubts}! \\ $$
