
Question Number 53376 by rajeshghorai130@gmail.com last updated on 21/Jan/19
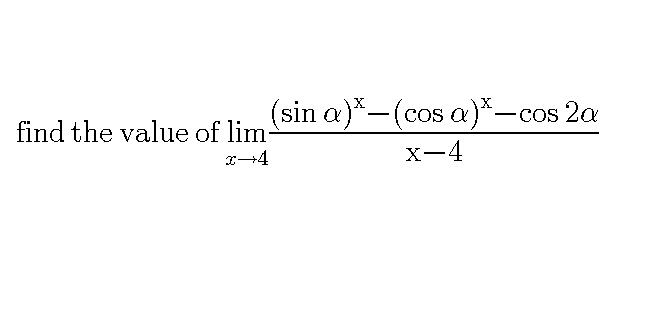
Commented by Abdo msup. last updated on 21/Jan/19
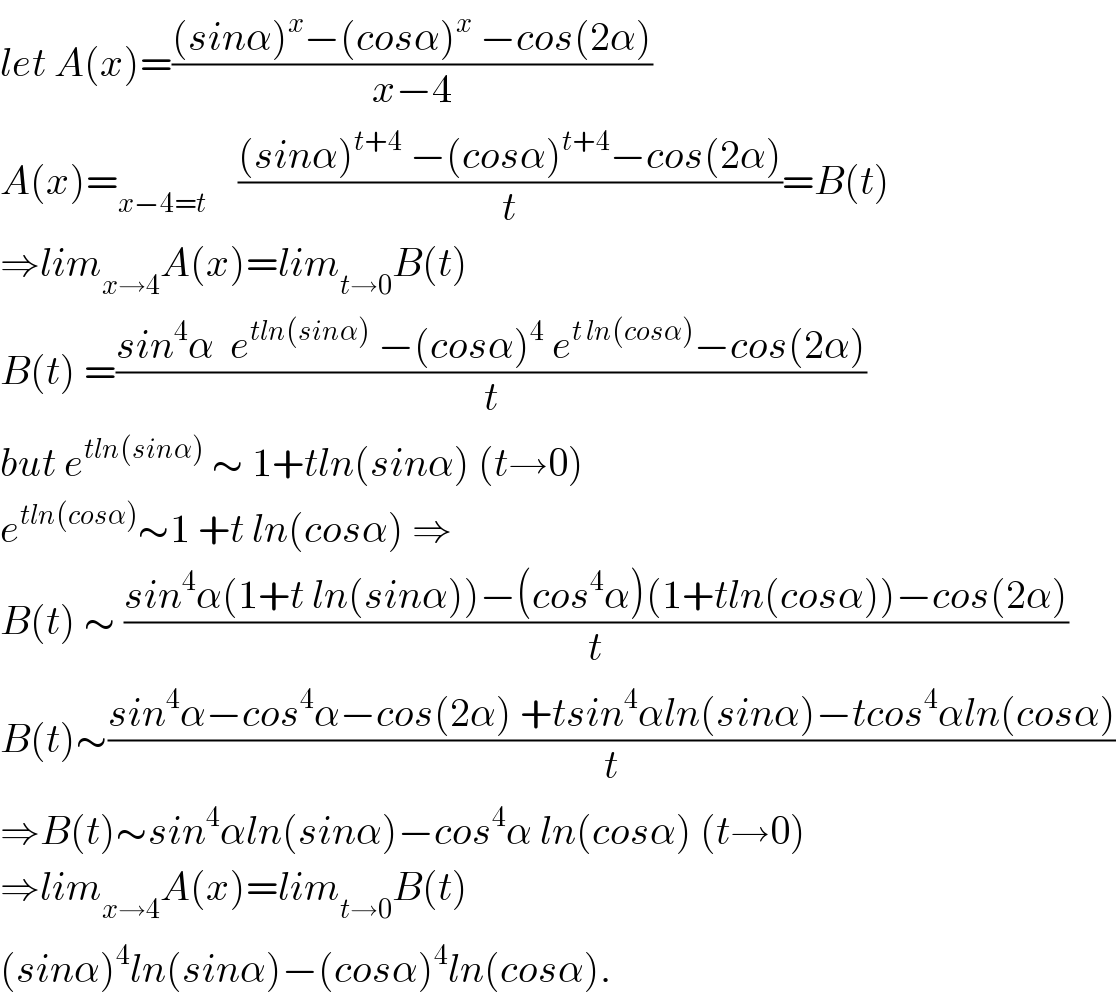
$${let}\:{A}\left({x}\right)=\frac{\left({sin}\alpha\right)^{{x}} −\left({cos}\alpha\right)^{{x}} \:−{cos}\left(\mathrm{2}\alpha\right)}{{x}−\mathrm{4}} \\ $$$${A}\left({x}\right)=_{{x}−\mathrm{4}={t}} \:\:\:\:\frac{\left({sin}\alpha\right)^{{t}+\mathrm{4}} \:−\left({cos}\alpha\right)^{{t}+\mathrm{4}} −{cos}\left(\mathrm{2}\alpha\right)}{{t}}={B}\left({t}\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{4}} {A}\left({x}\right)={lim}_{{t}\rightarrow\mathrm{0}} {B}\left({t}\right)\: \\ $$$${B}\left({t}\right)\:=\frac{{sin}^{\mathrm{4}} \alpha\:\:{e}^{{tln}\left({sin}\alpha\right)} \:−\left({cos}\alpha\right)^{\mathrm{4}} \:{e}^{{t}\:{ln}\left({cos}\alpha\right)} −{cos}\left(\mathrm{2}\alpha\right)}{{t}} \\ $$$${but}\:{e}^{{tln}\left({sin}\alpha\right)} \:\sim\:\mathrm{1}+{tln}\left({sin}\alpha\right)\:\left({t}\rightarrow\mathrm{0}\right) \\ $$$${e}^{{tln}\left({cos}\alpha\right)} \sim\mathrm{1}\:+{t}\:{ln}\left({cos}\alpha\right)\:\Rightarrow \\ $$$${B}\left({t}\right)\:\sim\:\frac{{sin}^{\mathrm{4}} \alpha\left(\mathrm{1}+{t}\:{ln}\left({sin}\alpha\right)\right)−\left({cos}^{\mathrm{4}} \alpha\right)\left(\mathrm{1}+{tln}\left({cos}\alpha\right)\right)−{cos}\left(\mathrm{2}\alpha\right)}{{t}} \\ $$$${B}\left({t}\right)\sim\frac{{sin}^{\mathrm{4}} \alpha−{cos}^{\mathrm{4}} \alpha−{cos}\left(\mathrm{2}\alpha\right)\:+{tsin}^{\mathrm{4}} \alpha{ln}\left({sin}\alpha\right)−{tcos}^{\mathrm{4}} \alpha{ln}\left({cos}\alpha\right)}{{t}} \\ $$$$\Rightarrow{B}\left({t}\right)\sim{sin}^{\mathrm{4}} \alpha{ln}\left({sin}\alpha\right)−{cos}^{\mathrm{4}} \alpha\:{ln}\left({cos}\alpha\right)\:\left({t}\rightarrow\mathrm{0}\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{4}} {A}\left({x}\right)={lim}_{{t}\rightarrow\mathrm{0}} {B}\left({t}\right) \\ $$$$\left({sin}\alpha\right)^{\mathrm{4}} {ln}\left({sin}\alpha\right)−\left({cos}\alpha\right)^{\mathrm{4}} {ln}\left({cos}\alpha\right). \\ $$
Answered by pooja24 last updated on 21/Jan/19
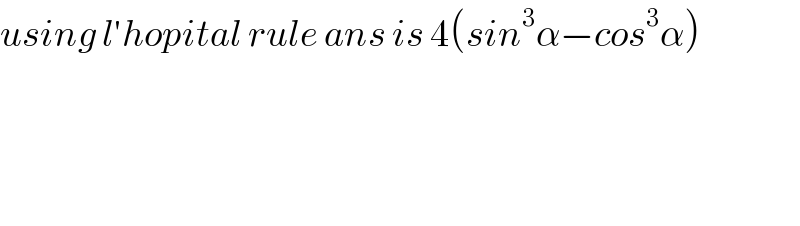
$${using}\:{l}'{hopital}\:{rule}\:{ans}\:{is}\:\mathrm{4}\left({sin}^{\mathrm{3}} \alpha−{cos}^{\mathrm{3}} \alpha\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19

$${i}\:{think}\:{question}\:{should}\:{be} \\ $$$$\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\frac{\left({sin}\alpha\right)^{{x}} −\left({cos}\alpha\right)^{{x}} +{cos}\mathrm{2}\alpha}{{x}−\mathrm{4}}\left(\frac{\mathrm{0}}{\mathrm{0}}\right){form} \\ $$$${using}\:{LH}\:{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\frac{\left({sin}\alpha\right)^{{x}} {lnsin}\alpha−\left({cos}\alpha\right)^{{x}} {lncos}\alpha}{\mathrm{1}} \\ $$$$=\left({sin}\alpha\right)^{\mathrm{4}} {lnsin}\alpha−\left({cos}\alpha\right)^{\mathrm{4}} {lncos}\alpha \\ $$$$ \\ $$
Commented by rajeshghorai130@gmail.com last updated on 21/Jan/19
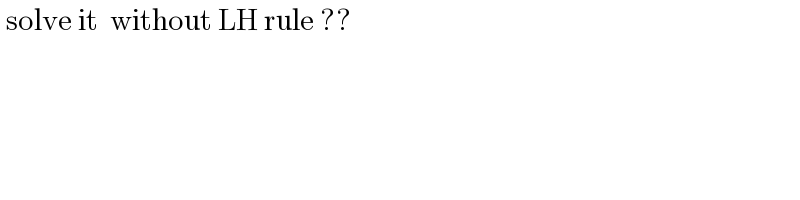
$$\:\mathrm{solve}\:\mathrm{it}\:\:\mathrm{without}\:\mathrm{LH}\:\mathrm{rule}\:?? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19

$${is}\:{it}\:{a}\:{request}...{language}..{seem}\:{otherwise} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19
![without LH rule... t=x−4 lim_(t→0) (((sinα)^(t+4) −(cosα)^(t+4) +cos^2 α−sin^2 α)/t) lim_(t→0) (((sin^ α)^(t+4) −(cosα)^(t+4) +(cos^2 α−sin^2 α)(cos^2 α+sin^2 α)←tricks)/t) =lim_(t→0) [((sin^4 α(sin^t α−1))/t)−((cos^4 α(cos^t α−1))/t)] =sin^4 α×lnsinα−cos^4 α×lncosα( proved) used formula lim_(x→0) ((a^x −1)/x)=lna N li_(x→0) lim_(x→0) ((a^x −1)/x) =li_(x→0)](Q53425.png)
$${without}\:{LH}\:{rule}... \\ $$$${t}={x}−\mathrm{4} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({sin}\alpha\right)^{{t}+\mathrm{4}} −\left({cos}\alpha\right)^{{t}+\mathrm{4}} +{cos}^{\mathrm{2}} \alpha−{sin}^{\mathrm{2}} \alpha}{{t}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({sin}^{} \alpha\right)^{{t}+\mathrm{4}} −\left({cos}\alpha\right)^{{t}+\mathrm{4}} +\left({cos}^{\mathrm{2}} \alpha−{sin}^{\mathrm{2}} \alpha\right)\left({cos}^{\mathrm{2}} \alpha+{sin}^{\mathrm{2}} \alpha\right)\leftarrow{tricks}}{{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{{sin}^{\mathrm{4}} \alpha\left({sin}^{{t}} \alpha−\mathrm{1}\right)}{{t}}−\frac{{cos}^{\mathrm{4}} \alpha\left({cos}^{{t}} \alpha−\mathrm{1}\right)}{{t}}\right] \\ $$$$={sin}^{\mathrm{4}} \alpha×{lnsin}\alpha−{cos}^{\mathrm{4}} \alpha×{lncos}\alpha\left(\:{proved}\right) \\ $$$${used}\:{formula} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{a}^{{x}} −\mathrm{1}}{{x}}={lna} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\mathbb{N} \\ $$$$ \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{a}^{{x}} −\mathrm{1}}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$
