
Question Number 53358 by gunawan last updated on 20/Jan/19
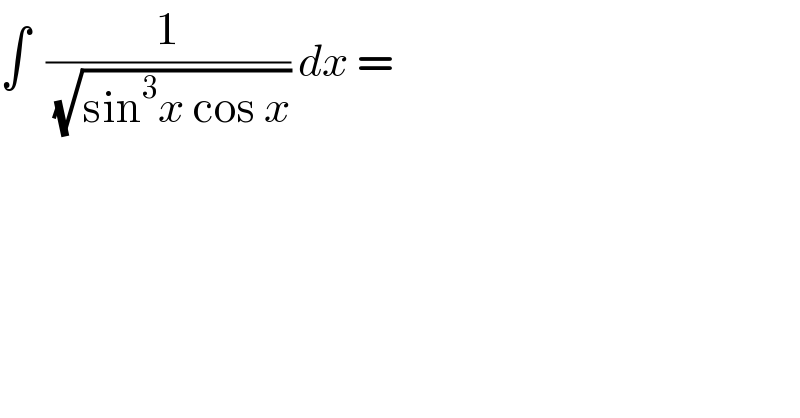
$$\int\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{sin}^{\mathrm{3}} {x}\:\mathrm{cos}\:{x}}}\:{dx}\:= \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19
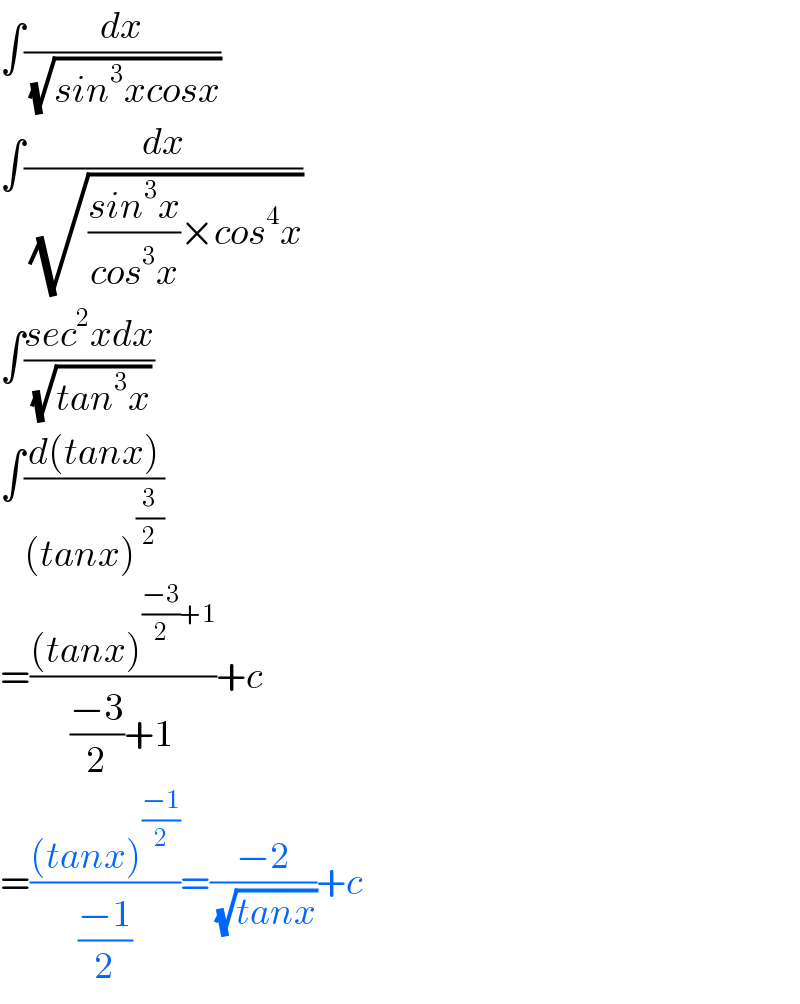
$$\int\frac{{dx}}{\sqrt{{sin}^{\mathrm{3}} {xcosx}}} \\ $$$$\int\frac{{dx}}{\sqrt{\frac{{sin}^{\mathrm{3}} {x}}{{cos}^{\mathrm{3}} {x}}×{cos}^{\mathrm{4}} {x}}} \\ $$$$\int\frac{{sec}^{\mathrm{2}} {xdx}}{\sqrt{{tan}^{\mathrm{3}} {x}}} \\ $$$$\int\frac{{d}\left({tanx}\right)}{\left({tanx}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\left({tanx}\right)^{\frac{−\mathrm{3}}{\mathrm{2}}+\mathrm{1}} }{\frac{−\mathrm{3}}{\mathrm{2}}+\mathrm{1}}+{c} \\ $$$$=\frac{\left({tanx}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} }{\frac{−\mathrm{1}}{\mathrm{2}}}=\frac{−\mathrm{2}}{\sqrt{{tanx}}}+{c} \\ $$
