
Question Number 53270 by Abdo msup. last updated on 19/Jan/19
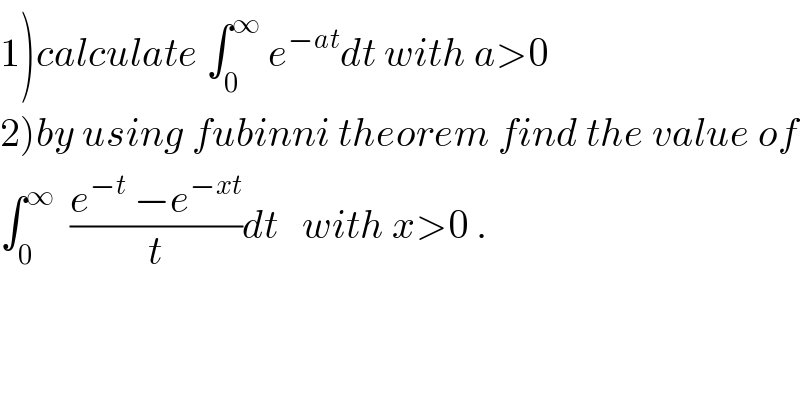
$$\left.\mathrm{1}\right){calculate}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{at}} {dt}\:{with}\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right){by}\:{using}\:{fubinni}\:{theorem}\:{find}\:{the}\:{value}\:{of} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{t}} \:−{e}^{−{xt}} }{{t}}{dt}\:\:\:{with}\:{x}>\mathrm{0}\:. \\ $$
Commented bymaxmathsup by imad last updated on 20/Jan/19
![1) ∫_0 ^∞ e^(−at) dt =[−(1/a) e^(−at) ]_0 ^(+∞) =(1/a) 2) ⇒∫_1 ^x (da/a) =ln(x) we take x>0 but ∫_1 ^x (da/a) =∫_1 ^x (∫_0 ^∞ e^(−at) dt)da =∫_0 ^∞ (∫_1 ^x e^(−at) da)dt ( fubini theorem) =∫_0 ^∞ ( [−(1/t)e^(−at) ]_(a=1) ^(a=x) )dt =∫_0 ^∞ ((e^(−t) −e^(−xt) )/t) dt ⇒ ∫_0 ^∞ ((e^(−t) −e^(−xt) )/t) dt =ln(x) with x>0](Q53312.png)
$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{at}} {dt}\:=\left[−\frac{\mathrm{1}}{{a}}\:{e}^{−{at}} \right]_{\mathrm{0}} ^{+\infty} \:=\frac{\mathrm{1}}{{a}} \\ $$ $$\left.\mathrm{2}\right)\:\Rightarrow\int_{\mathrm{1}} ^{{x}} \:\frac{{da}}{{a}}\:={ln}\left({x}\right)\:\:\:\:\:\:{we}\:{take}\:{x}>\mathrm{0}\:{but} \\ $$ $$\int_{\mathrm{1}} ^{{x}} \:\frac{{da}}{{a}}\:=\int_{\mathrm{1}} ^{{x}} \left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{at}} {dt}\right){da}\:=\int_{\mathrm{0}} ^{\infty} \:\left(\int_{\mathrm{1}} ^{{x}} \:{e}^{−{at}} {da}\right){dt}\:\:\:\left(\:{fubini}\:{theorem}\right) \\ $$ $$=\int_{\mathrm{0}} ^{\infty} \:\left(\:\left[−\frac{\mathrm{1}}{{t}}{e}^{−{at}} \right]_{{a}=\mathrm{1}} ^{{a}={x}} \right){dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{t}} −{e}^{−{xt}} }{{t}}\:{dt}\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{t}} \:−{e}^{−{xt}} }{{t}}\:{dt}\:={ln}\left({x}\right)\:\:\:{with}\:{x}>\mathrm{0} \\ $$
Answered by kaivan.ahmadi last updated on 19/Jan/19
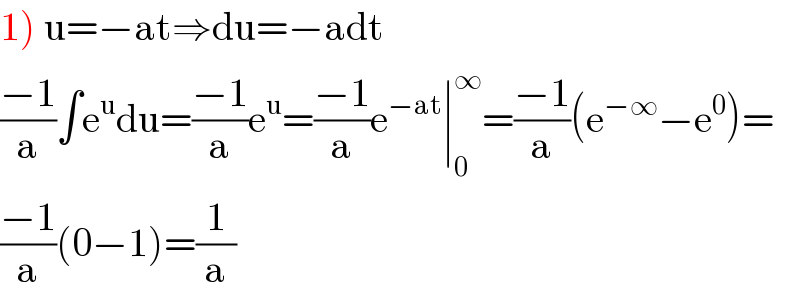
$$\left.\mathrm{1}\right)\:\mathrm{u}=−\mathrm{at}\Rightarrow\mathrm{du}=−\mathrm{adt} \\ $$ $$\frac{−\mathrm{1}}{\mathrm{a}}\int\mathrm{e}^{\mathrm{u}} \mathrm{du}=\frac{−\mathrm{1}}{\mathrm{a}}\mathrm{e}^{\mathrm{u}} =\frac{−\mathrm{1}}{\mathrm{a}}\mathrm{e}^{−\mathrm{at}} \mid_{\mathrm{0}} ^{\infty} =\frac{−\mathrm{1}}{\mathrm{a}}\left(\mathrm{e}^{−\infty} −\mathrm{e}^{\mathrm{0}} \right)= \\ $$ $$\frac{−\mathrm{1}}{\mathrm{a}}\left(\mathrm{0}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{a}} \\ $$
