
Question Number 53261 by Abdo msup. last updated on 19/Jan/19
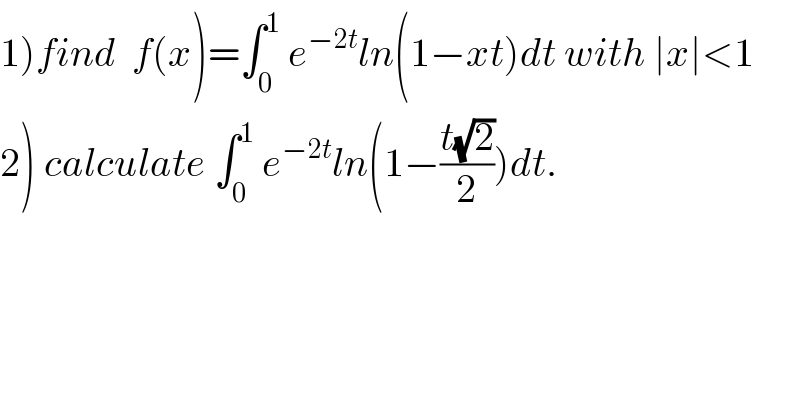
$$\left.\mathrm{1}\right){find}\:\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−{xt}\right){dt}\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{t}} {ln}\left(\mathrm{1}−\frac{{t}\sqrt{\mathrm{2}}}{\mathrm{2}}\right){dt}. \\ $$
