
Question Number 53144 by mr W last updated on 18/Jan/19

$${Find}\:{all}\:{integers}\:{x}\:{and}\:{y}\:{such}\:{that} \\ $$$$\frac{{xy}}{{x}+{y}}\:{is}\:{also}\:{integer}. \\ $$
Commented by mr W last updated on 19/Jan/19

$$\boldsymbol{{x}}=\left(\boldsymbol{{i}}+\mathrm{1}\right)\boldsymbol{{j}} \\ $$$$\boldsymbol{{y}}=\boldsymbol{{i}}\left(\boldsymbol{{i}}+\mathrm{1}\right)\boldsymbol{{j}} \\ $$$$\boldsymbol{{i}},\boldsymbol{{j}}\:\in\:\mathbb{Z} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jan/19
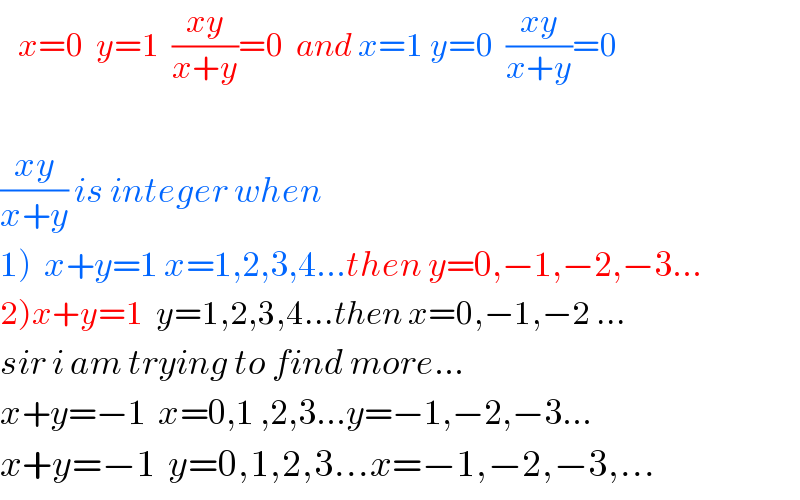
$$\:\:\:{x}=\mathrm{0}\:\:{y}=\mathrm{1}\:\:\frac{{xy}}{{x}+{y}}=\mathrm{0}\:\:{and}\:{x}=\mathrm{1}\:{y}=\mathrm{0}\:\:\frac{{xy}}{{x}+{y}}=\mathrm{0} \\ $$$$ \\ $$$$\frac{{xy}}{{x}+{y}}\:{is}\:{integer}\:{when} \\ $$$$\left.\mathrm{1}\right)\:\:{x}+{y}=\mathrm{1}\:{x}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}...{then}\:{y}=\mathrm{0},−\mathrm{1},−\mathrm{2},−\mathrm{3}... \\ $$$$\left.\mathrm{2}\right){x}+{y}=\mathrm{1}\:\:{y}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}...{then}\:{x}=\mathrm{0},−\mathrm{1},−\mathrm{2}\:... \\ $$$${sir}\:{i}\:{am}\:{trying}\:{to}\:{find}\:{more}... \\ $$$${x}+{y}=−\mathrm{1}\:\:{x}=\mathrm{0},\mathrm{1}\:,\mathrm{2},\mathrm{3}...{y}=−\mathrm{1},−\mathrm{2},−\mathrm{3}... \\ $$$${x}+{y}=−\mathrm{1}\:\:{y}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3}...{x}=−\mathrm{1},−\mathrm{2},−\mathrm{3},... \\ $$
Commented by mr W last updated on 18/Jan/19

$${thanks}\:{for}\:{trying}! \\ $$$${can}\:{you}\:{give}\:{a}\:{general}\:{solution}\:{for} \\ $$$${all}\:{solutions}? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Jan/19

$${sir}\:{i}\:{am}\:{trying}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Jan/19

$${i}\:{think}\:{general}\:{solution}\:{related}\:{to}\:{greatest}\:{integer} \\ $$$${function}...{better}\:{you}\:{post}\:{genetal}\:{solution}\:{sir}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${and}\: \\ $$
Answered by ajfour last updated on 18/Jan/19
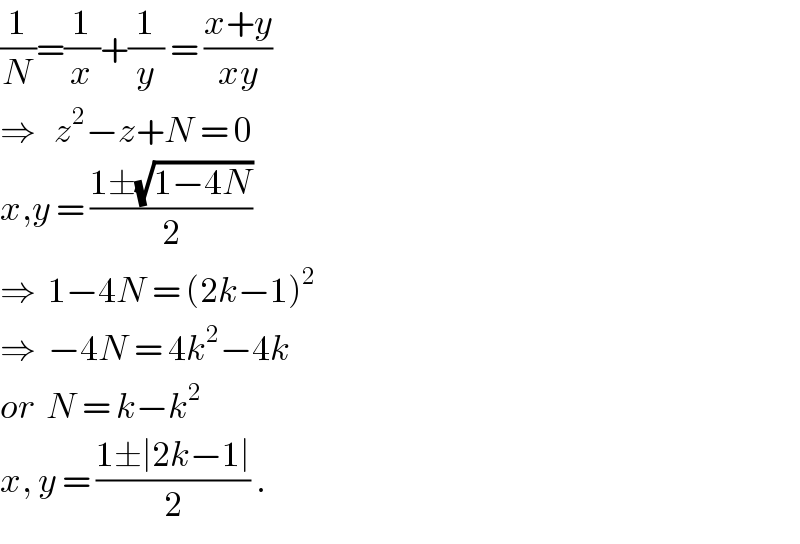
$$\frac{\mathrm{1}}{{N}}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:=\:\frac{{x}+{y}}{{xy}} \\ $$$$\Rightarrow\:\:\:{z}^{\mathrm{2}} −{z}+{N}\:=\:\mathrm{0} \\ $$$${x},{y}\:=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}{N}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{1}−\mathrm{4}{N}\:=\:\left(\mathrm{2}{k}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:−\mathrm{4}{N}\:=\:\mathrm{4}{k}^{\mathrm{2}} −\mathrm{4}{k} \\ $$$${or}\:\:{N}\:=\:{k}−{k}^{\mathrm{2}} \\ $$$${x},\:{y}\:=\:\frac{\mathrm{1}\pm\mid\mathrm{2}{k}−\mathrm{1}\mid}{\mathrm{2}}\:.\:\:\:\:\:\:\: \\ $$
Commented by ajfour last updated on 18/Jan/19

$${will}\:{this}\:{do}\:{Sir}\:? \\ $$
Commented by mr W last updated on 18/Jan/19

$${it}\:{describs}\:{only}\:{some}\:{solutions},\:{i}.{e}. \\ $$$${those}\:{with}\:{x}+{y}=\mathrm{1} \\ $$$${but}\:{not}\:{all}\:{solutions},\:{so}\:{it}\:{is}\:{not} \\ $$$${a}\:{general}\:{solution}\:{sir},\:{e}.{g}. \\ $$$${following}\:{solutions}\:{are}\:{correct},\:{but}\:{they} \\ $$$${can}\:{not}\:{be}\:{obtained}\:{from}\:{your}\:{formula}: \\ $$$${x}=\mathrm{2},\:{y}=\mathrm{2} \\ $$$${x}=\mathrm{3},\:{y}=\mathrm{6} \\ $$
Commented by ajfour last updated on 18/Jan/19
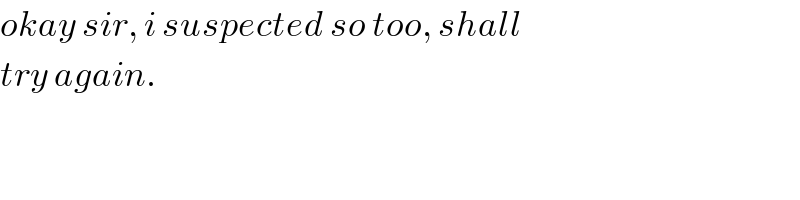
$${okay}\:{sir},\:{i}\:{suspected}\:{so}\:{too},\:{shall} \\ $$$${try}\:{again}. \\ $$
