
Question Number 53118 by gunawan last updated on 18/Jan/19
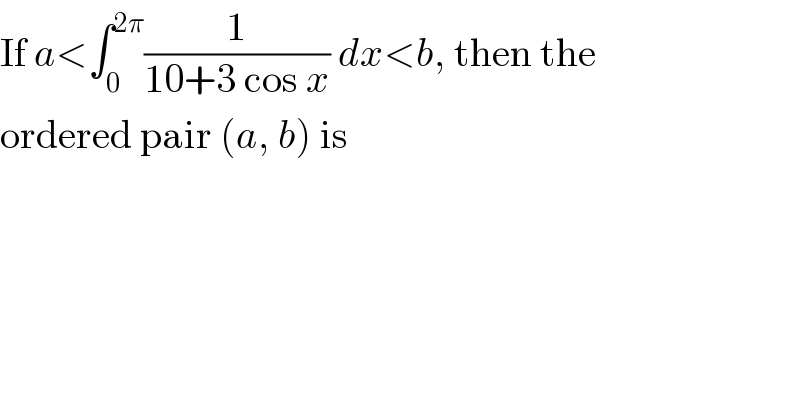
$$\mathrm{If}\:{a}<\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{\mathrm{10}+\mathrm{3}\:\mathrm{cos}\:{x}}\:{dx}<{b},\:\mathrm{then}\:\mathrm{the} \\ $$ $$\mathrm{ordered}\:\mathrm{pair}\:\left({a},\:{b}\right)\:\mathrm{is} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jan/19

$${i}\:{am}\:{using}\:{simple}\:{logic}.. \\ $$ $${then}\:{i}\left[{shall}\:{solve}\:{in}\:{details}\right. \\ $$ $${we}\:{know}\:\:{cosx}\:{max}\:{value}=+\mathrm{1} \\ $$ $${cosx}\:{minimum}\:{value}=−\mathrm{1} \\ $$ $${so} \\ $$ $$\:\mathrm{10}+\mathrm{3}\left(\mathrm{1}\right)>\mathrm{10}+\mathrm{3}{cosx}>\mathrm{10}+\mathrm{3}\left(−\mathrm{1}\right) \\ $$ $$\mathrm{13}>\mathrm{10}+\mathrm{3}{cosx}>\mathrm{7} \\ $$ $$\frac{\mathrm{1}}{\mathrm{13}}<\frac{\mathrm{1}}{\mathrm{10}+\mathrm{3}{cosx}}<\frac{\mathrm{1}}{\mathrm{7}} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\mathrm{13}}<\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\mathrm{10}+\mathrm{3}{cosx}}<\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\mathrm{7}} \\ $$ $$\frac{\mathrm{2}\pi}{\mathrm{13}}<\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\mathrm{10}+\mathrm{3}{cosx}}<\frac{\mathrm{2}\pi}{\mathrm{7}} \\ $$ $${so}\:{a}=\frac{\mathrm{2}\pi}{\mathrm{13}}\:\:\:{b}=\frac{\mathrm{2}\pi}{\mathrm{7}}\:\:\:\:\left(\frac{\mathrm{2}\pi}{\mathrm{13}},\frac{\mathrm{2}\pi}{\mathrm{7}}\right) \\ $$
Commented bygunawan last updated on 19/Jan/19
$$\mathrm{wow}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

$${most}\:{welcome}... \\ $$
