
Question Number 52891 by ajfour last updated on 14/Jan/19

Commented by ajfour last updated on 15/Jan/19
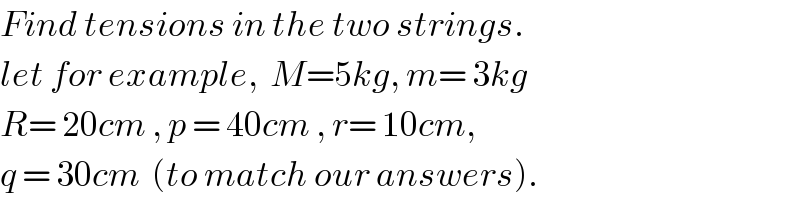
$${Find}\:{tensions}\:{in}\:{the}\:{two}\:{strings}. \\ $$$${let}\:{for}\:{example},\:\:{M}=\mathrm{5}{kg},\:{m}=\:\mathrm{3}{kg} \\ $$$${R}=\:\mathrm{20}{cm}\:,\:{p}\:=\:\mathrm{40}{cm}\:,\:{r}=\:\mathrm{10}{cm}, \\ $$$${q}\:=\:\mathrm{30}{cm}\:\:\left({to}\:{match}\:{our}\:{answers}\right). \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
![T_a cosα−Mg−N_m sinθ=0.....eqn1 T_a sinα+N_m cosθ=N_w eqn 2 sinα=(R/(a+R)) T_b sinβ−mg−N_m sinθ=0 .....eqn3 T_b cosβ=N_m cosθ....eqn4 cosγ=(((a+R)^2 +(b+r)^2 −(r+R)^2 )/(2(a+R)(b+r)))←known value β=90^o −(α+γ) sinθ=(h/(r+R)) h=(a+R)cosα−(b+r)sinβ to solve...four eqn...pls wait... pls check upto this.... [after checking ] (T_b /(cosθ))=(N_m /(cosβ))=k T_b =kcosθ N_m =kcosβ T_b sinβ−N_m sinθ=mg kcosθsinβ−kcosβsinθ=mg k=((mg)/(sin(β−θ))) T_b =((mgcosθ)/(sin(β−θ))) N_m =((mgcosβ)/(sin(β−θ))) T_a =((Mg+N_m sinθ)/(cosα)) =((Mg+((mgcosβ)/(sin(β−θ)))sinθ)/(cosα)) =((Mgsin(β−θ)+mgcosβsinθ)/(cosαsin(β−θ))) now something to say... 1)T_a =depends on M,m,α,β,θ 2)T_b =depends on m,θ,β sinα=(R/(a+R)) ←known value angle γ also known cosγ=(((a+R)^2 +(b+r)^2 −(R+r)^2 )/(2(a+R)(b+r))) β=90^o −(α+γ) ←so β is known sinθ=(h/(r+R)) h=(a+R)cosα−(b+r)sinβ sinθ=(((a+R)cosα−(b+r)sinβ)/(r+R))←known value T_a =((Mgsin(β−θ)+mgcosβsinθ)/(cos∝sin(β−θ))) T_b =((mgcosθ)/(sin(β−θ))) comments...since T_a and T_b depends on α,β,θ but the value of α,β,θ are already calculated by the given parameters(a,b,r,R) so i think problem is solved... if we put value of (α,β,θ) in expression of T_a and T_b ...it will be more lengthy and zargon](Q52904.png)
$${T}_{{a}} {cos}\alpha−{Mg}−{N}_{{m}} {sin}\theta=\mathrm{0}.....{eqn}\mathrm{1} \\ $$$${T}_{{a}} {sin}\alpha+{N}_{{m}} {cos}\theta={N}_{{w}} \:\:\:\:{eqn}\:\:\:\mathrm{2} \\ $$$${sin}\alpha=\frac{{R}}{{a}+{R}} \\ $$$${T}_{{b}} {sin}\beta−{mg}−{N}_{{m}} {sin}\theta=\mathrm{0}\:.....{eqn}\mathrm{3} \\ $$$${T}_{{b}} {cos}\beta={N}_{{m}} {cos}\theta....{eqn}\mathrm{4} \\ $$$${cos}\gamma=\frac{\left({a}+{R}\right)^{\mathrm{2}} +\left({b}+{r}\right)^{\mathrm{2}} −\left({r}+{R}\right)^{\mathrm{2}} }{\mathrm{2}\left({a}+{R}\right)\left({b}+{r}\right)}\leftarrow{known}\:{value} \\ $$$$\beta=\mathrm{90}^{{o}} −\left(\alpha+\gamma\right) \\ $$$${sin}\theta=\frac{{h}}{{r}+{R}} \\ $$$${h}=\left({a}+{R}\right){cos}\alpha−\left({b}+{r}\right){sin}\beta \\ $$$${to}\:{solve}...{four}\:{eqn}...{pls}\:{wait}... \\ $$$${pls}\:{check}\:{upto}\:{this}.... \\ $$$$\left[{after}\:{checking}\:\right] \\ $$$$\frac{{T}_{{b}} }{{cos}\theta}=\frac{{N}_{{m}} }{{cos}\beta}={k} \\ $$$${T}_{{b}} ={kcos}\theta\:\:\:\:\:\:{N}_{{m}} ={kcos}\beta \\ $$$${T}_{{b}} {sin}\beta−{N}_{{m}} {sin}\theta={mg} \\ $$$${kcos}\theta{sin}\beta−{kcos}\beta{sin}\theta={mg} \\ $$$${k}=\frac{{mg}}{{sin}\left(\beta−\theta\right)} \\ $$$${T}_{{b}} =\frac{{mgcos}\theta}{{sin}\left(\beta−\theta\right)}\:\:\:\:{N}_{{m}} =\frac{{mgcos}\beta}{{sin}\left(\beta−\theta\right)} \\ $$$$ \\ $$$$ \\ $$$${T}_{{a}} =\frac{{Mg}+{N}_{{m}} {sin}\theta}{{cos}\alpha} \\ $$$$\:\:\:=\frac{{Mg}+\frac{{mgcos}\beta}{{sin}\left(\beta−\theta\right)}{sin}\theta}{{cos}\alpha} \\ $$$$=\frac{{Mgsin}\left(\beta−\theta\right)+{mgcos}\beta{sin}\theta}{{cos}\alpha{sin}\left(\beta−\theta\right)} \\ $$$${now}\:{something}\:{to}\:{say}... \\ $$$$\left.\mathrm{1}\right){T}_{{a}} ={depends}\:{on}\:\:{M},{m},\alpha,\beta,\theta \\ $$$$\left.\mathrm{2}\right){T}_{{b}} ={depends}\:{on}\:{m},\theta,\beta \\ $$$${sin}\alpha=\frac{{R}}{{a}+{R}}\:\leftarrow{known}\:{value} \\ $$$$ \\ $$$${angle}\:\gamma\:{also}\:{known} \\ $$$${cos}\gamma=\frac{\left({a}+{R}\right)^{\mathrm{2}} +\left({b}+{r}\right)^{\mathrm{2}} −\left({R}+{r}\right)^{\mathrm{2}} }{\mathrm{2}\left({a}+{R}\right)\left({b}+{r}\right)} \\ $$$$ \\ $$$$\beta=\mathrm{90}^{{o}} −\left(\alpha+\gamma\right)\:\leftarrow{so}\:\beta\:{is}\:{known} \\ $$$$ \\ $$$${sin}\theta=\frac{{h}}{{r}+{R}} \\ $$$${h}=\left({a}+{R}\right){cos}\alpha−\left({b}+{r}\right){sin}\beta \\ $$$${sin}\theta=\frac{\left({a}+{R}\right){cos}\alpha−\left({b}+{r}\right){sin}\beta}{{r}+{R}}\leftarrow{known}\:{value} \\ $$$$\boldsymbol{{T}}_{{a}} =\frac{{Mgsin}\left(\beta−\theta\right)+{mgcos}\beta{sin}\theta}{{cos}\propto{sin}\left(\beta−\theta\right)} \\ $$$${T}_{{b}} =\frac{{mgcos}\theta}{{sin}\left(\beta−\theta\right)} \\ $$$${comments}...{since}\:{T}_{{a}} \:{and}\:{T}_{{b}} \:{depends}\:{on}\:\alpha,\beta,\theta \\ $$$${but}\:{the}\:{value}\:{of}\:\alpha,\beta,\theta\:{are}\:{already}\:{calculated} \\ $$$${by}\:{the}\:{given}\:{parameters}\left({a},{b},{r},{R}\right) \\ $$$${so}\:{i}\:{think}\:{problem}\:{is}\:{solved}... \\ $$$${if}\:{we}\:{put}\:{value}\:{of}\:\left(\alpha,\beta,\theta\right)\:{in}\:{expression}\:{of}\:{T}_{{a}} \\ $$$${and}\:{T}_{{b}} ...\boldsymbol{{it}}\:\boldsymbol{{will}}\:\boldsymbol{{be}}\:\boldsymbol{{more}}\:\boldsymbol{{lengthy}}\:\boldsymbol{{and}}\:\boldsymbol{{zargon}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 15/Jan/19

$${remove}\:{the}\:{intermediaries}\:{sir}, \\ $$$${seek}\:{help}\:{from}\:{torque}\:{equations}, \\ $$$${may}\:{be}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19

$${thank}\:{you}... \\ $$
Commented by ajfour last updated on 15/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19

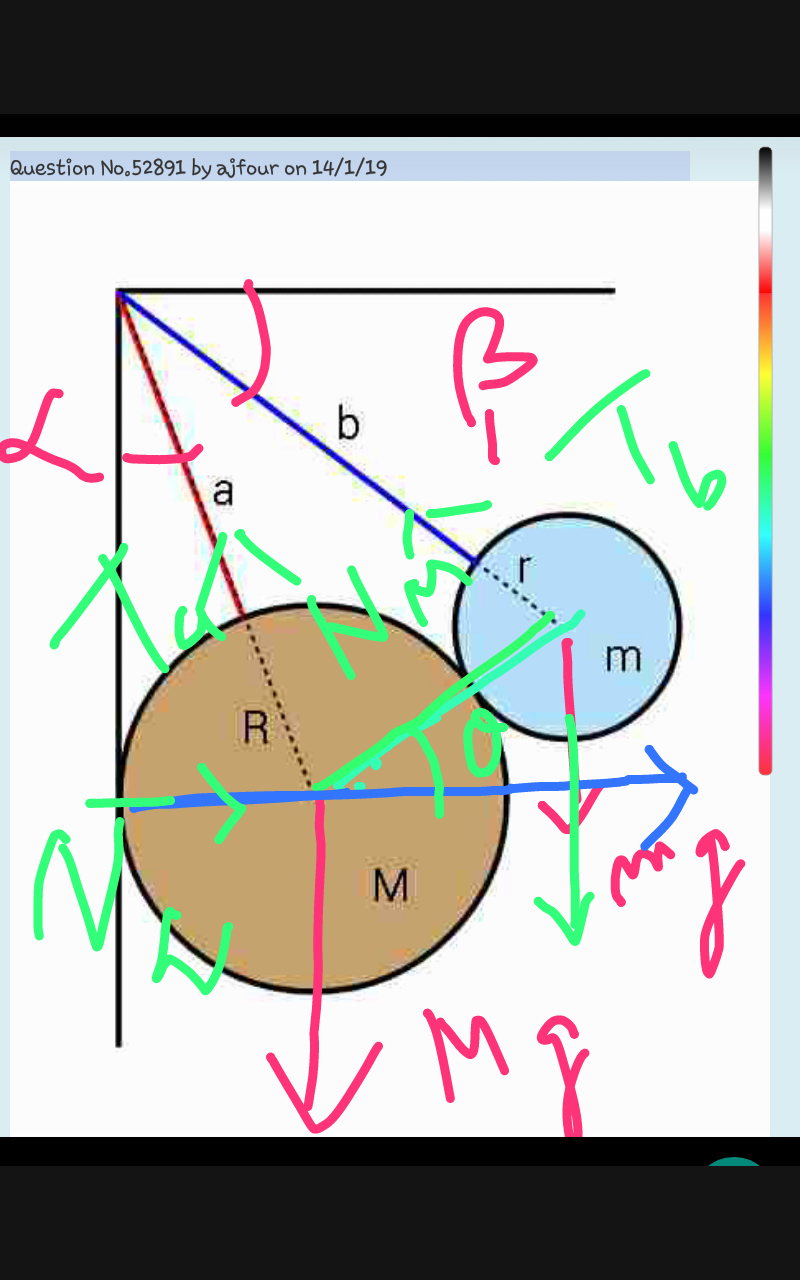
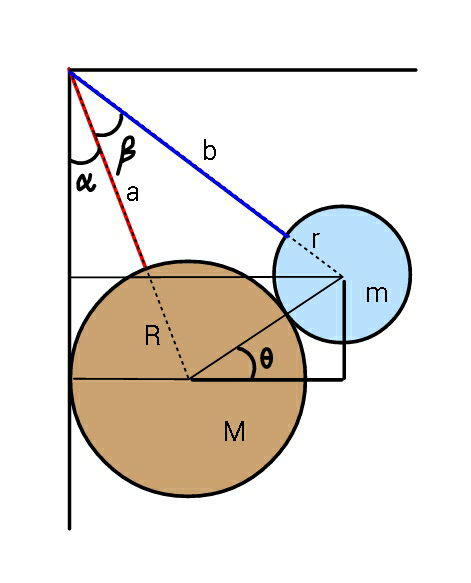
$${how}\:{you}\:{draw}\:{this}\:{diagram}... \\ $$
Commented by ajfour last updated on 15/Jan/19
cos θ +[sin (α+β)](R+r)sin θ} = mg(R+r)cos θ ⇒ T_b = ((mgcos θ)/(cos (α+β−θ))) T_a = (((M+m)g−((mgcos θcos (α+β))/(cos (α+β−θ))))/(cos α)) I obtain: α≈ 19.4712° , β ≈ 26.384°, θ≈ 73.135° , and with g=10m/s^2 , T_b ≈ 9.7926N T_a ≈ 77.6189N .](Q52931.png)
$$\mathrm{sin}\:\alpha\:=\:\frac{{R}}{{a}+{R}} \\ $$$$\mathrm{cos}\:\beta\:=\:\frac{\left({a}+{R}\right)^{\mathrm{2}} +\left({b}+{r}\right)^{\mathrm{2}} −\left({R}+{r}\right)^{\mathrm{2}} }{\mathrm{2}\left({a}+{R}\right)\left({b}+{r}\right)} \\ $$$$\mathrm{tan}\:\theta\:=\:\frac{\left({a}+{R}\right)\mathrm{cos}\:\alpha−\left({b}+{r}\right)\mathrm{cos}\:\left(\alpha+\beta\right)}{\left({b}+{r}\right)\mathrm{sin}\:\left(\alpha+\beta\right)−\left({a}+{R}\right)\mathrm{sin}\:\alpha} \\ $$$${T}_{{a}} \mathrm{cos}\:\alpha+{T}_{{b}} \mathrm{cos}\:\left(\alpha+\beta\right)=\left({M}+{m}\right){g} \\ $$$${taking}\:{moment}\:{about}\:{center}\:{of} \\ $$$${bigger}\:{body}: \\ $$$${T}_{{b}} \left\{\left[\mathrm{cos}\:\left(\alpha+\beta\right)\right]\left({R}+{r}\right)\mathrm{cos}\:\theta\right. \\ $$$$\left.\:\:\:+\left[\mathrm{sin}\:\left(\alpha+\beta\right)\right]\left({R}+{r}\right)\mathrm{sin}\:\theta\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{mg}\left({R}+{r}\right)\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{T}_{{b}} \:=\:\frac{{mg}\mathrm{cos}\:\theta}{\mathrm{cos}\:\left(\alpha+\beta−\theta\right)} \\ $$$$\:\:\:\:\:\:\:{T}_{{a}} \:=\:\frac{\left({M}+{m}\right){g}−\frac{{mg}\mathrm{cos}\:\theta\mathrm{cos}\:\left(\alpha+\beta\right)}{\mathrm{cos}\:\left(\alpha+\beta−\theta\right)}}{\mathrm{cos}\:\alpha} \\ $$$${I}\:{obtain}: \\ $$$$\:\:\:\alpha\approx\:\mathrm{19}.\mathrm{4712}°\:\:,\:\beta\:\approx\:\mathrm{26}.\mathrm{384}°, \\ $$$$\:\:\theta\approx\:\mathrm{73}.\mathrm{135}°\:,\:{and}\:{with}\:\:{g}=\mathrm{10}{m}/{s}^{\mathrm{2}} , \\ $$$$\:\:\:\boldsymbol{{T}}_{\boldsymbol{{b}}} \approx\:\mathrm{9}.\mathrm{7926}{N} \\ $$$$\:\:\:\boldsymbol{{T}}_{\boldsymbol{{a}}} \approx\:\mathrm{77}.\mathrm{6189}{N}\:. \\ $$
Commented by ajfour last updated on 15/Jan/19
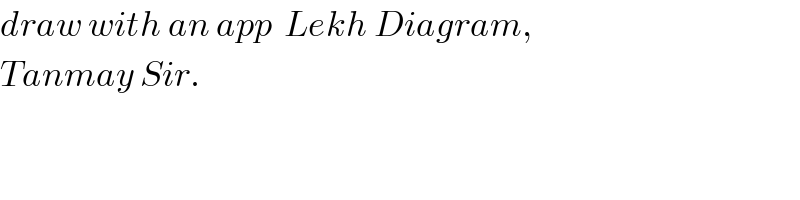
$${draw}\:{with}\:{an}\:{app}\:\:{Lekh}\:{Diagram}, \\ $$$${Tanmay}\:{Sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
$${ok}\:{i}\:{shall}\:{download}\:{it}... \\ $$
Answered by mr W last updated on 15/Jan/19
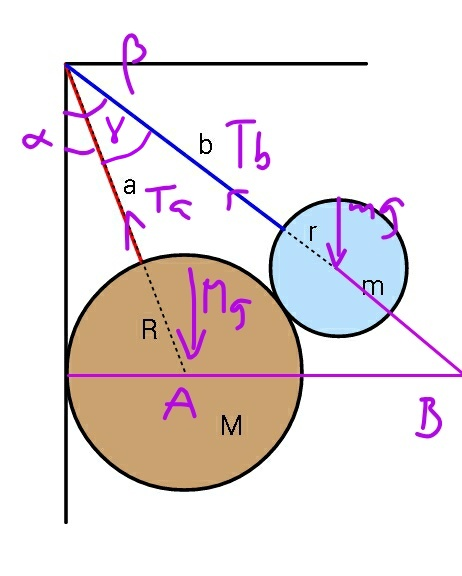
Commented by mr W last updated on 15/Jan/19
![α=sin^(−1) (R/(a+R)) γ=cos^(−1) (((a+R)^2 +(b+r)^2 −(R+r)^2 )/(2(a+R)(b+r))) β=α+γ=sin^(−1) (R/(a+R))+cos^(−1) (((a+R)^2 +(b+r)^2 −(R+r)^2 )/(2(a+R)(b+r))) ΣM_A =0: T_b (a+R) sin γ=mg [(b+r) sin β−R] ⇒T_a =(((b+r) sin β−R)/((a+R) sin γ))×mg ΣM_B =0: T_a [(((a+R) cos α sin γ)/(cos β))]=Mg[(a+R) cos α tan β−R]+mg[(a+R) cos α tan β−(b+r) sin β] ⇒T_a =(({Mg[(a+R) cos α tan β−R]+mg[(a+R) cos α tan β−(b+r) sin β]}cos β)/((a+R) cos α sin γ))](Q52917.png)
$$\alpha=\mathrm{sin}^{−\mathrm{1}} \frac{{R}}{{a}+{R}} \\ $$$$\gamma=\mathrm{cos}^{−\mathrm{1}} \frac{\left({a}+{R}\right)^{\mathrm{2}} +\left({b}+{r}\right)^{\mathrm{2}} −\left({R}+{r}\right)^{\mathrm{2}} }{\mathrm{2}\left({a}+{R}\right)\left({b}+{r}\right)} \\ $$$$\beta=\alpha+\gamma=\mathrm{sin}^{−\mathrm{1}} \frac{{R}}{{a}+{R}}+\mathrm{cos}^{−\mathrm{1}} \frac{\left({a}+{R}\right)^{\mathrm{2}} +\left({b}+{r}\right)^{\mathrm{2}} −\left({R}+{r}\right)^{\mathrm{2}} }{\mathrm{2}\left({a}+{R}\right)\left({b}+{r}\right)} \\ $$$$ \\ $$$$\Sigma{M}_{{A}} =\mathrm{0}: \\ $$$${T}_{{b}} \:\left({a}+{R}\right)\:\mathrm{sin}\:\gamma={mg}\:\left[\left({b}+{r}\right)\:\mathrm{sin}\:\beta−{R}\right] \\ $$$$\Rightarrow{T}_{{a}} =\frac{\left({b}+{r}\right)\:\mathrm{sin}\:\beta−{R}}{\left({a}+{R}\right)\:\mathrm{sin}\:\gamma}×{mg} \\ $$$$\Sigma{M}_{{B}} =\mathrm{0}: \\ $$$${T}_{{a}} \left[\frac{\left({a}+{R}\right)\:\mathrm{cos}\:\alpha\:\mathrm{sin}\:\gamma}{\mathrm{cos}\:\beta}\right]={Mg}\left[\left({a}+{R}\right)\:\mathrm{cos}\:\alpha\:\mathrm{tan}\:\beta−{R}\right]+{mg}\left[\left({a}+{R}\right)\:\mathrm{cos}\:\alpha\:\mathrm{tan}\:\beta−\left({b}+{r}\right)\:\mathrm{sin}\:\beta\right] \\ $$$$\Rightarrow{T}_{{a}} =\frac{\left\{{Mg}\left[\left({a}+{R}\right)\:\mathrm{cos}\:\alpha\:\mathrm{tan}\:\beta−{R}\right]+{mg}\left[\left({a}+{R}\right)\:\mathrm{cos}\:\alpha\:\mathrm{tan}\:\beta−\left({b}+{r}\right)\:\mathrm{sin}\:\beta\right]\right\}\mathrm{cos}\:\beta}{\left({a}+{R}\right)\:\mathrm{cos}\:\alpha\:\mathrm{sin}\:\gamma} \\ $$
Commented by ajfour last updated on 15/Jan/19

$${Great}\:{way}\:{Sir}! \\ $$
