
Question Number 52881 by ajfour last updated on 14/Jan/19
Commented by ajfour last updated on 14/Jan/19
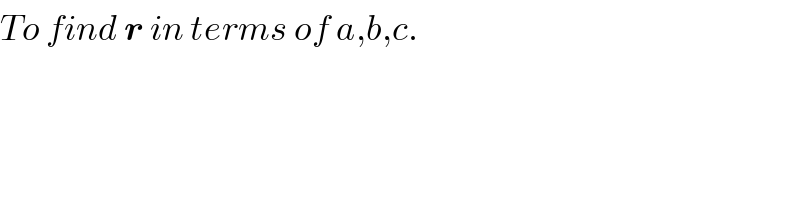
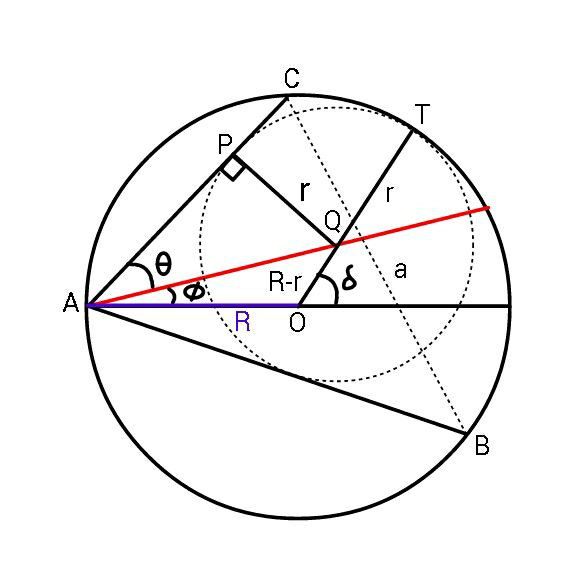
$${To}\:{find}\:\boldsymbol{{r}}\:{in}\:{terms}\:{of}\:{a},{b},{c}. \\ $$
Commented by mr W last updated on 14/Jan/19
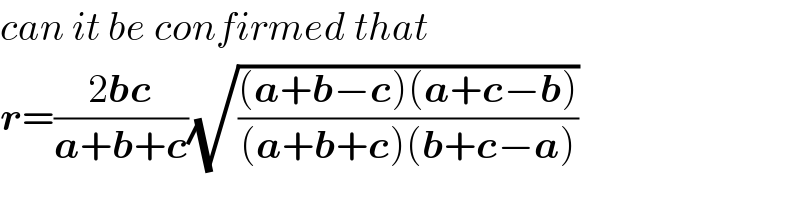
$${can}\:{it}\:{be}\:{confirmed}\:{that} \\ $$$$\boldsymbol{{r}}=\frac{\mathrm{2}\boldsymbol{{bc}}}{\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}}\sqrt{\frac{\left(\boldsymbol{{a}}+\boldsymbol{{b}}−\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}−\boldsymbol{{b}}\right)}{\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}} \\ $$
Commented by ajfour last updated on 14/Jan/19
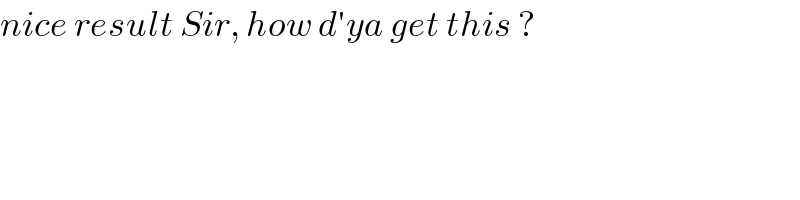
$${nice}\:{result}\:{Sir},\:{how}\:{d}'{ya}\:{get}\:{this}\:? \\ $$
Commented by behi83417@gmail.com last updated on 14/Jan/19
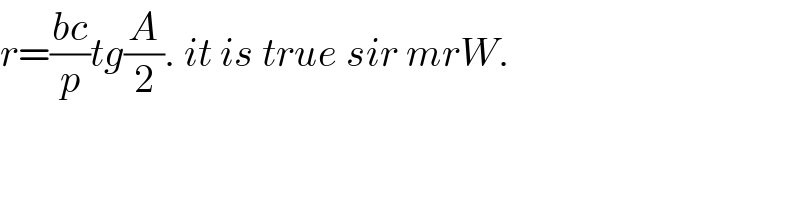
$${r}=\frac{{bc}}{{p}}{tg}\frac{{A}}{\mathrm{2}}.\:{it}\:{is}\:{true}\:{sir}\:{mrW}. \\ $$
Commented by MJS last updated on 14/Jan/19

$$...\mathrm{and}\:\mathrm{please}\:\mathrm{re}−\mathrm{check}\:\mathrm{52061},\:\mathrm{I}\:\mathrm{get}\:\mathrm{a}\:\mathrm{different} \\ $$$$\mathrm{result} \\ $$
Commented by MJS last updated on 14/Jan/19

$$\mathrm{see}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{qu}.\:\mathrm{52806} \\ $$
Commented by mr W last updated on 15/Jan/19
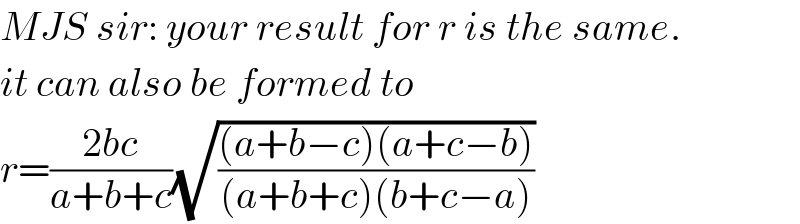
$${MJS}\:{sir}:\:{your}\:{result}\:{for}\:{r}\:{is}\:{the}\:{same}. \\ $$$${it}\:{can}\:{also}\:{be}\:{formed}\:{to} \\ $$$${r}=\frac{\mathrm{2}{bc}}{{a}+{b}+{c}}\sqrt{\frac{\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)}{\left({a}+{b}+{c}\right)\left({b}+{c}−{a}\right)}} \\ $$
Commented by mr W last updated on 15/Jan/19
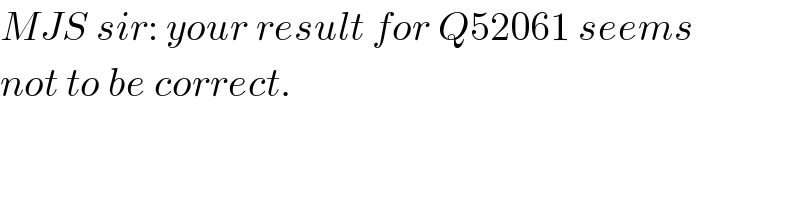
$${MJS}\:{sir}:\:{your}\:{result}\:{for}\:{Q}\mathrm{52061}\:{seems} \\ $$$${not}\:{to}\:{be}\:{correct}. \\ $$
Commented by MJS last updated on 15/Jan/19

$$\mathrm{I}\:\mathrm{will}\:\mathrm{look}\:\mathrm{into}\:\mathrm{52061}\:\mathrm{once}\:\mathrm{more} \\ $$$$\mathrm{I}\:\mathrm{saw}\:\mathrm{that}\:\mathrm{the}\:\mathrm{other}\:\mathrm{result}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{yours}, \\ $$$$\mathrm{I}\:\mathrm{thought}\:\mathrm{you}\:\mathrm{might}\:\mathrm{have}\:\mathrm{achieved}\:\mathrm{it}\:\mathrm{throuhh} \\ $$$$\mathrm{a}\:\mathrm{different}\:\mathrm{path} \\ $$
Answered by ajfour last updated on 15/Jan/19

$${From}\:{power}\:{of}\:{point}\:{Q}\:{w}.{r}.{t}.\: \\ $$$${circumcircle}: \\ $$$$\:\:\:\left(\mathrm{2}{R}\mathrm{cos}\:\phi−\frac{{r}}{\mathrm{sin}\:\theta}\right)\frac{{r}}{\mathrm{sin}\:\theta}\:=\:{r}\left(\mathrm{2}{R}−{r}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\mathrm{2}{R}\mathrm{cos}\:\phi\:=\:\frac{{r}}{\mathrm{sin}\:\theta}+\left(\mathrm{2}{R}−{r}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......\left({i}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${further}\:\:\:{R}\mathrm{cos}\:\left(\theta+\phi\right)=\frac{{b}}{\mathrm{2}}\:\:\:\& \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{R}\mathrm{cos}\:\left(\theta−\phi\right)=\frac{{c}}{\mathrm{2}} \\ $$$${Adding}:\:\:\:\mathrm{2}{R}\mathrm{cos}\:\phi\mathrm{cos}\:\theta=\frac{{b}+{c}}{\mathrm{2}} \\ $$$${So}\:\:{using}\:\left({i}\right) \\ $$$$\:\frac{{r}}{\mathrm{tan}\:\theta}+{R}\mathrm{sin}\:\mathrm{2}\theta−\frac{{r}\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{tan}\:\theta}=\frac{{b}+{c}}{\mathrm{2}} \\ $$$${but}\:\:\:\frac{\mathrm{sin}\:\mathrm{2}\theta}{{a}}\:=\:\frac{\mathrm{1}}{\mathrm{2}{R}}\:\:\:\:\Rightarrow \\ $$$$\:\:\frac{\boldsymbol{{rcos}}^{\mathrm{2}} \boldsymbol{\theta}}{\boldsymbol{{tan}}\:\boldsymbol{\theta}}\:=\frac{\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{r}}\:=\:\frac{\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}{\mathrm{1}+\boldsymbol{{cos}}\:{A}}\sqrt{\frac{\mathrm{1}−\boldsymbol{{cos}}\:{A}}{\mathrm{1}+\boldsymbol{{cos}}\:{A}}} \\ $$$$\:\:\:\:\:\:=\:\frac{\left({b}+{c}−{a}\right)}{\left(\frac{\mathrm{2}{bc}+{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\right)}\sqrt{\frac{\mathrm{2}{bc}−{b}^{\mathrm{2}} −{c}^{\mathrm{2}} +{a}^{\mathrm{2}} }{\mathrm{2}{bc}+{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }} \\ $$$$\boldsymbol{{r}}\:=\:\frac{\mathrm{2}\boldsymbol{{bc}}}{\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)}\sqrt{\frac{\left(\boldsymbol{{a}}+\boldsymbol{{b}}−\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}−\boldsymbol{{b}}\right)}{\left(\boldsymbol{{b}}+\boldsymbol{{c}}+\boldsymbol{{a}}\right)\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}}\:. \\ $$
Commented by mr W last updated on 15/Jan/19
����������
