
Question Number 52103 by Gulay last updated on 03/Jan/19
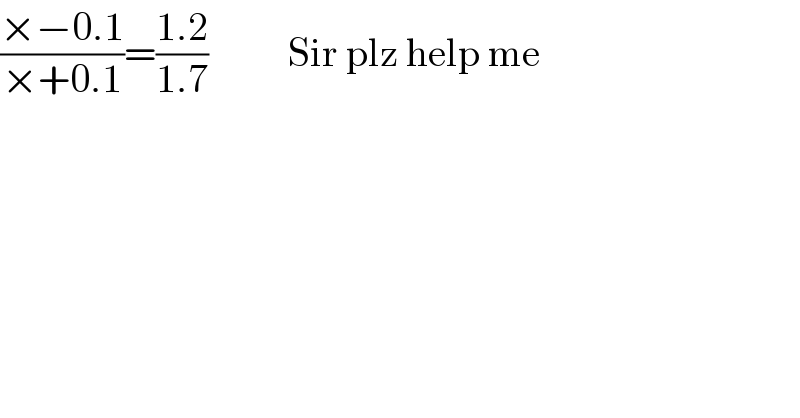
$$\frac{×−\mathrm{0}.\mathrm{1}}{×+\mathrm{0}.\mathrm{1}}=\frac{\mathrm{1}.\mathrm{2}}{\mathrm{1}.\mathrm{7}}\:\:\:\:\:\:\:\:\:\:\mathrm{Sir}\:\mathrm{plz}\:\mathrm{help}\:\mathrm{me} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jan/19
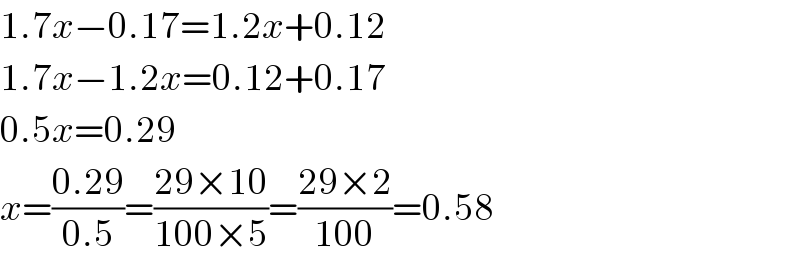
$$\mathrm{1}.\mathrm{7}{x}−\mathrm{0}.\mathrm{17}=\mathrm{1}.\mathrm{2}{x}+\mathrm{0}.\mathrm{12} \\ $$$$\mathrm{1}.\mathrm{7}{x}−\mathrm{1}.\mathrm{2}{x}=\mathrm{0}.\mathrm{12}+\mathrm{0}.\mathrm{17} \\ $$$$\mathrm{0}.\mathrm{5}{x}=\mathrm{0}.\mathrm{29} \\ $$$${x}=\frac{\mathrm{0}.\mathrm{29}}{\mathrm{0}.\mathrm{5}}=\frac{\mathrm{29}×\mathrm{10}}{\mathrm{100}×\mathrm{5}}=\frac{\mathrm{29}×\mathrm{2}}{\mathrm{100}}=\mathrm{0}.\mathrm{58} \\ $$
Commented by Gulay last updated on 06/Jan/19
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
Answered by $@ty@m last updated on 03/Jan/19

$${by}\:{componendo}\:\&\:{dividendo} \\ $$$$\frac{{x}−\mathrm{0}.\mathrm{1}+{x}+\mathrm{0}.\mathrm{1}}{{x}−\mathrm{0}.\mathrm{1}−{x}−\mathrm{0}.\mathrm{1}}=\frac{\mathrm{1}.\mathrm{2}+\mathrm{1}.\mathrm{7}}{\mathrm{1}.\mathrm{2}−\mathrm{1}.\mathrm{7}} \\ $$$$\frac{\mathrm{2}{x}}{−\mathrm{0}.\mathrm{2}}=\frac{\mathrm{2}.\mathrm{9}}{−\mathrm{0}.\mathrm{5}} \\ $$$${x}=\frac{\mathrm{29}}{\mathrm{5}}×\mathrm{0}.\mathrm{1}=\mathrm{0}.\mathrm{58} \\ $$
