Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 105289 by Anindita last updated on 27/Jul/20

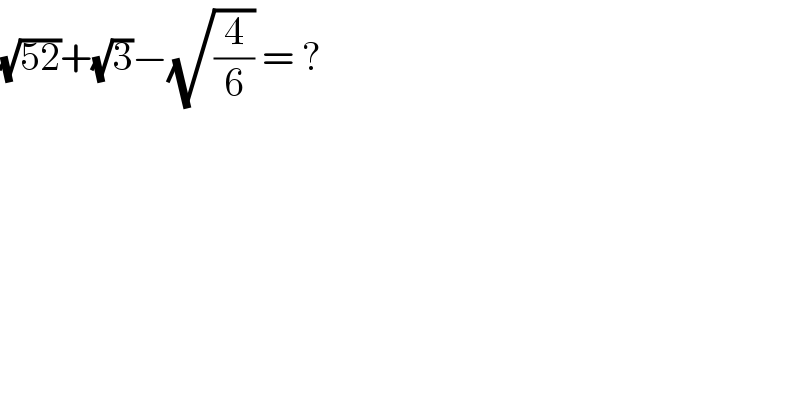
(√(52))+(√3)−(√(4/6)) = ?

$$\sqrt{\mathrm{52}}+\sqrt{\mathrm{3}}−\sqrt{\frac{\mathrm{4}}{\mathrm{6}}}\:=\:? \\ $$

Answered by SUMIT007 last updated on 27/Jul/20

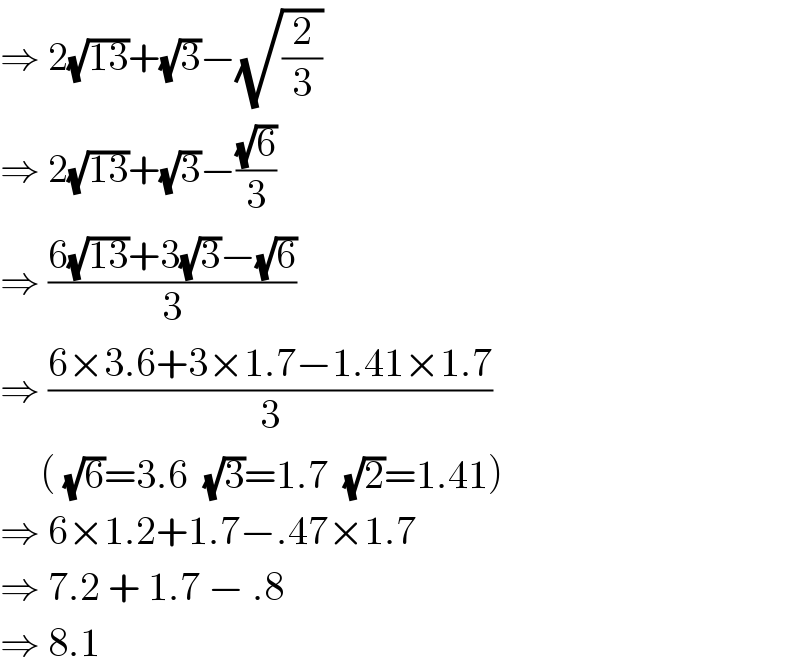
⇒ 2(√(13))+(√3)−(√(2/3)) ⇒ 2(√(13))+(√3)−((√6)/3) ⇒ ((6(√(13))+3(√3)−(√6))/3) ⇒ ((6×3.6+3×1.7−1.41×1.7)/3) ( (√6)=3.6 (√3)=1.7 (√2)=1.41) ⇒ 6×1.2+1.7−.47×1.7 ⇒ 7.2 + 1.7 − .8 ⇒ 8.1

$$\Rightarrow\:\mathrm{2}\sqrt{\mathrm{13}}+\sqrt{\mathrm{3}}−\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\Rightarrow\:\mathrm{2}\sqrt{\mathrm{13}}+\sqrt{\mathrm{3}}−\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\Rightarrow\:\frac{\mathrm{6}\sqrt{\mathrm{13}}+\mathrm{3}\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\Rightarrow\:\frac{\mathrm{6}×\mathrm{3}.\mathrm{6}+\mathrm{3}×\mathrm{1}.\mathrm{7}−\mathrm{1}.\mathrm{41}×\mathrm{1}.\mathrm{7}}{\mathrm{3}}\: \\ $$$$\:\:\:\:\:\left(\:\sqrt{\mathrm{6}}=\mathrm{3}.\mathrm{6}\:\:\sqrt{\mathrm{3}}=\mathrm{1}.\mathrm{7}\:\:\sqrt{\mathrm{2}}=\mathrm{1}.\mathrm{41}\right) \\ $$$$\Rightarrow\:\mathrm{6}×\mathrm{1}.\mathrm{2}+\mathrm{1}.\mathrm{7}−.\mathrm{47}×\mathrm{1}.\mathrm{7} \\ $$$$\Rightarrow\:\mathrm{7}.\mathrm{2}\:+\:\mathrm{1}.\mathrm{7}\:−\:.\mathrm{8} \\ $$$$\Rightarrow\:\mathrm{8}.\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com