
Question Number 5195 by sanusihammed last updated on 29/Apr/16

Commented by FilupSmith last updated on 29/Apr/16
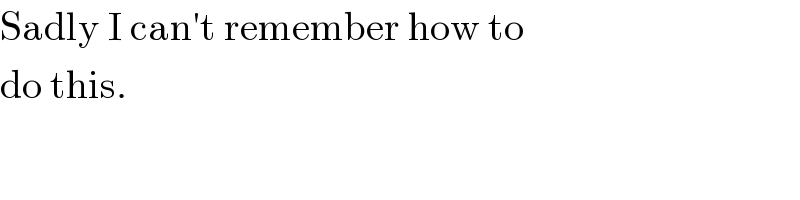
$$\mathrm{Sadly}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{remember}\:\mathrm{how}\:\mathrm{to} \\ $$$$\mathrm{do}\:\mathrm{this}. \\ $$
Answered by prakash jain last updated on 30/Apr/16

$$\mathrm{Numbers}\:\mathrm{are}\:\mathrm{not}\:\mathrm{quite}\:\mathrm{readble},\:\mathrm{in}\:\mathrm{your}\:\mathrm{diagram} \\ $$$$ \\ $$$$\mathrm{R2}\:\mathrm{and}\:\mathrm{R3}\:\mathrm{is}\:\mathrm{connected}\:\mathrm{in}\:\mathrm{series}\:=\mathrm{R}_{\mathrm{23}} =\mathrm{R2}+\mathrm{R3} \\ $$$$\mathrm{R4}\:\mathrm{and}\:\mathrm{R5}\:\mathrm{is}\:\mathrm{connected}\:\mathrm{in}\:\mathrm{series}\:=\mathrm{R}_{\mathrm{45}} =\mathrm{R4}+\mathrm{R5} \\ $$$$\mathrm{R}_{\mathrm{23}} \:\mathrm{and}\:\mathrm{R}_{\mathrm{45}} \:\mathrm{are}\:\mathrm{in}\:\mathrm{parallel} \\ $$$$\frac{\mathrm{1}}{\mathrm{R}_{\mathrm{2345}} }=\frac{\mathrm{1}}{\mathrm{R}_{\mathrm{23}} }+\frac{\mathrm{1}}{\mathrm{R}_{\mathrm{45}} } \\ $$$$\mathrm{R}_{\mathrm{2345}} =\frac{\mathrm{R}_{\mathrm{23}} \mathrm{R}_{\mathrm{45}} }{\mathrm{R}_{\mathrm{23}} +\mathrm{R}_{\mathrm{4v}} } \\ $$$$\mathrm{R}_{\mathrm{2345}} \:\mathrm{is}\:\mathrm{connected}\:\mathrm{in}\:\mathrm{series}\:\mathrm{with}\:\mathrm{R}_{\mathrm{1}} \\ $$$$\mathrm{Net}\:\mathrm{Resistance}=\mathrm{R}_{\mathrm{eq}} =\mathrm{R}_{\mathrm{2345}} +\mathrm{R}_{\mathrm{1}} \\ $$$$\mathrm{Current}\:\mathrm{from}\:\mathrm{battery}=\mathrm{I}=\frac{\mathrm{12}}{\mathrm{R}_{\mathrm{eq}} } \\ $$$$\mathrm{Current}\:\mathrm{thru}\:\mathrm{R}_{\mathrm{1}} =\mathrm{I} \\ $$$$\mathrm{Potential}\:\mathrm{difference}\:\mathrm{across}\:\mathrm{R}_{\mathrm{2345}} =\mathrm{V}_{\mathrm{1}} =\mathrm{12}−\mathrm{IR}_{\mathrm{1}} \\ $$$$\mathrm{current}\:\mathrm{thru}\:\mathrm{R}_{\mathrm{23}} =\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{V}_{\mathrm{1}} }{\mathrm{R}_{\mathrm{23}} } \\ $$$$\mathrm{current}\:\mathrm{thru}\:\mathrm{R}_{\mathrm{45}} =\mathrm{I}_{\mathrm{2}} =\frac{\mathrm{V}_{\mathrm{1}} }{\mathrm{R}_{\mathrm{45}} } \\ $$$$\mathrm{current}\:\mathrm{thru}\:\mathrm{R}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{R}_{\mathrm{3}} =\mathrm{I}_{\mathrm{1}} \\ $$$$\mathrm{current}\:\mathrm{thru}\:\mathrm{R}_{\mathrm{4}} \:\mathrm{and}\:\mathrm{R}_{\mathrm{5}} =\mathrm{I}_{\mathrm{2}} \\ $$$$\mathrm{Power}\:=\mathrm{I}^{\mathrm{2}} \mathrm{R} \\ $$$$\mathrm{choose}\:\mathrm{I}\:\mathrm{based}\:\mathrm{and}\:\mathrm{which}\:\mathrm{resistor}\:\mathrm{is}\:\mathrm{2}\:\mathrm{ohm} \\ $$$$\mathrm{among}\:\mathrm{R}_{\mathrm{1}} \:\mathrm{to}\:\mathrm{R}_{\mathrm{5}} . \\ $$
Commented by prakash jain last updated on 30/Apr/16
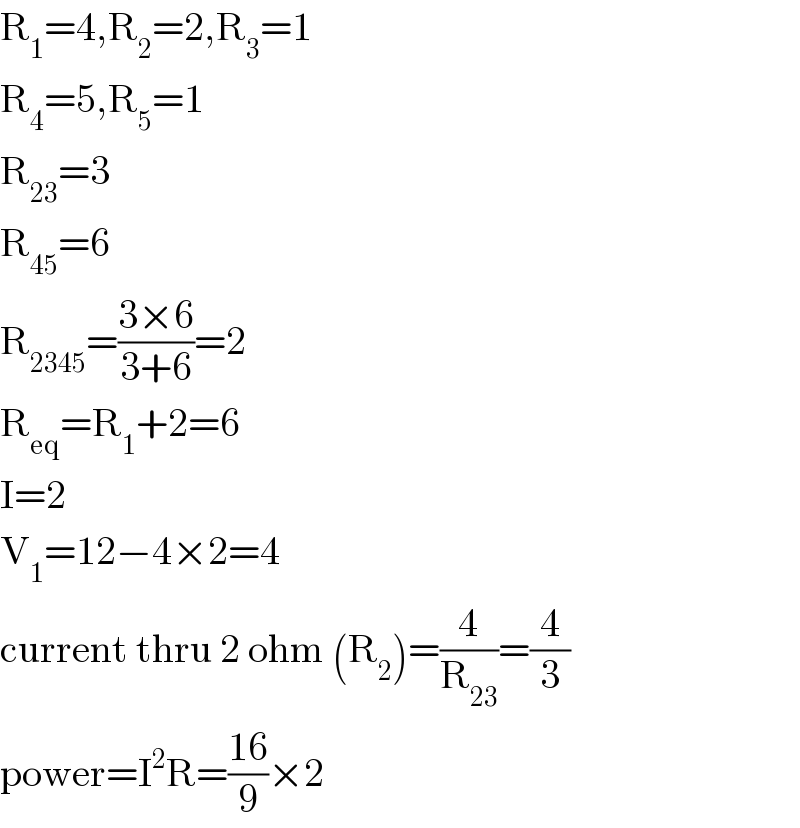
$$\mathrm{R}_{\mathrm{1}} =\mathrm{4},\mathrm{R}_{\mathrm{2}} =\mathrm{2},\mathrm{R}_{\mathrm{3}} =\mathrm{1} \\ $$$$\mathrm{R}_{\mathrm{4}} =\mathrm{5},\mathrm{R}_{\mathrm{5}} =\mathrm{1} \\ $$$$\mathrm{R}_{\mathrm{23}} =\mathrm{3} \\ $$$$\mathrm{R}_{\mathrm{45}} =\mathrm{6} \\ $$$$\mathrm{R}_{\mathrm{2345}} =\frac{\mathrm{3}×\mathrm{6}}{\mathrm{3}+\mathrm{6}}=\mathrm{2} \\ $$$$\mathrm{R}_{\mathrm{eq}} =\mathrm{R}_{\mathrm{1}} +\mathrm{2}=\mathrm{6} \\ $$$$\mathrm{I}=\mathrm{2} \\ $$$$\mathrm{V}_{\mathrm{1}} =\mathrm{12}−\mathrm{4}×\mathrm{2}=\mathrm{4} \\ $$$$\mathrm{current}\:\mathrm{thru}\:\mathrm{2}\:\mathrm{ohm}\:\left(\mathrm{R}_{\mathrm{2}} \right)=\frac{\mathrm{4}}{\mathrm{R}_{\mathrm{23}} }=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{power}=\mathrm{I}^{\mathrm{2}} \mathrm{R}=\frac{\mathrm{16}}{\mathrm{9}}×\mathrm{2} \\ $$
