
Question Number 51733 by Tinkutara last updated on 30/Dec/18
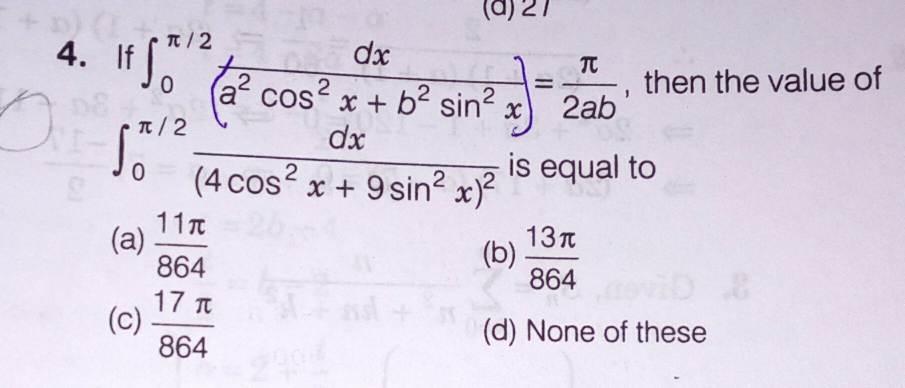
Commented by maxmathsup by imad last updated on 30/Dec/18

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{{a}^{\mathrm{2}} \frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:+{b}^{\mathrm{2}} \frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cos}\left(\mathrm{2}{x}\right)}\:=_{\mathrm{2}{x}={u}} \:\:\:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\:\frac{{du}}{\mathrm{2}\left(\:{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cosu}\right)} \\ $$$$=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\:\frac{{du}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cosu}}\:=_{{tan}\left(\frac{{u}}{\mathrm{2}}\right)={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{dt}}{\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}{a}^{\mathrm{2}} \:+\mathrm{2}{b}^{\mathrm{2}} {t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dt}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} {t}^{\mathrm{2}} }\:\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left.\mathrm{1}+\left(\frac{{b}}{{a}}{t}\right)^{\mathrm{2}} \right)}\:\:{with}\:{ab}>\mathrm{0} \\ $$$$=_{\frac{{b}}{{a}}{t}\:=\alpha} \:\:\:\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\frac{{a}}{{b}}\:{d}\alpha\:=\frac{\mathrm{1}}{{ab}}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{d}\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{ab}}.\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}{ab}}\:. \\ $$$${let}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}\:\Rightarrow{f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{−\mathrm{2}{acos}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}}{{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}−{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx} \\ $$$$=−\frac{\mathrm{2}}{{a}}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}\:+\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{1}−{cos}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx} \\ $$$$=−\frac{\mathrm{2}}{{a}}{f}\left({a}\right)\:+\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\:+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{−\mathrm{2}{acos}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx} \\ $$$${f}^{'} \left({a}\right)\:=−\frac{\mathrm{2}}{{a}}{f}\left({a}\right)\:+\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(...\right){dx}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{f}^{'} \left({a}\right)\:\Rightarrow \\ $$$$\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right){f}^{'} \left({a}\right)\:+\frac{\mathrm{2}}{{a}}{f}\left({a}\right)\:=\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}^{'} \left({a}\right)+\mathrm{2}{af}\left({a}\right)}{{a}^{\mathrm{2}} }\:=\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\:=\frac{{a}}{\mathrm{2}{b}^{\mathrm{2}} }\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left\{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){f}^{'} \left({a}\right)+\mathrm{2}{a}\:{f}\left({a}\right)\right\} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{ab}^{\mathrm{2}} }\left\{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\frac{\pi}{\mathrm{2}{b}}\left(\frac{−\mathrm{1}}{{a}^{\mathrm{2}} }\right)\:+\mathrm{2}{a}\:\frac{\pi}{\mathrm{2}{ab}}\right\}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ab}^{\mathrm{2}} }\left\{\:−\frac{\pi}{\mathrm{2}{a}^{\mathrm{2}} {b}}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:+\frac{\pi}{{b}}\right\} \\ $$$${a}=\mathrm{2}\:{and}\:{b}=\mathrm{3}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{\left(\mathrm{4}{cos}^{\mathrm{2}} {x}\:+\mathrm{9}{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}.\mathrm{9}}\left\{\frac{\pi\left(\mathrm{5}\right)}{\mathrm{8}.\mathrm{3}}\:+\frac{\pi}{\mathrm{3}}\right\}\:=\frac{\mathrm{1}}{\mathrm{36}}\left\{\frac{\mathrm{5}\pi}{\mathrm{24}}\:+\frac{\mathrm{8}\pi}{\mathrm{24}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{36}}\:.\frac{\mathrm{13}\pi}{\mathrm{24}}\:=\frac{\mathrm{13}\pi}{\mathrm{36}.\mathrm{24}}\:=\frac{\mathrm{13}\pi}{\mathrm{864}} \\ $$
Commented by Tinkutara last updated on 30/Dec/18
Thanks Sir!
Commented by turbo msup by abdo last updated on 30/Dec/18
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18
![∫_0 ^(π/2) (dx/(a^2 cos^2 x+b^2 sin^2 x)) ∫_0 ^(π/2) ((sec^2 xdx)/(a^2 +b^2 tan^2 x)) (1/b^2 )∫_0 ^(π/2) ((d(tanx))/(((a/b))^2 +tan^2 x)) (1/b^2 )×(1/(((a/b))))∣tan^(−1) (((tanx)/(a/b)))∣_0 ^(π/2) (1/(ab))[tan^(−1) (((tan(π/2))/(a/b)))−tan^(−1) ((0/(a/b)))] =(1/(ab))×tan^(−1) (∞)=(1/(ab))×(π/2)=(π/(2ab)) solving method−1 ∫_0 ^(π/2) (dx/((a^2 cos^2 x+b^2 sin^2 x)))=(π/(2ab)) diferentiate both side w.r.t a ∫_0 ^(π/2) (∂/∂a)[(/((a^2 cos^2 x+b^2 sin^2 x)))]dx=(π/(2b))×((−1)/a^2 ) ∫_0 ^(π/2) ((−1×2acos^2 x)/((a^2 cos^2 x+b^2 sin^2 x)^2 ))dx=((−π)/(2a^2 b)) ∫_0 ^(π/2) ((cos^2 xdx)/((a^2 cos^2 x+b^2 sin^2 x)^2 ))dx=(π/(4a^3 b)).....eqn p again diffdrentiate w.r.t b ∫_0 ^(π/2) ((−2bsin^2 x)/((a^2 cos^2 x+b^2 sin^2 x)^2 ))dx=((−π)/(2ab^2 )) ∫_0 ^(π/2) ((sin^2 x)/((a^2 cos^2 x+b^2 sin^2 x)^2 ))=(π/(4ab^3 )).....eqn q add eqn p and q ∫_0 ^(π/2) ((cos^2 x+sin^2 x)/((a^2 cos^2 x+b^2 sin^2 x)^2 ))dx=(π/(4ab))((1/a^2 )+(1/b^2 ))=((π(a^2 +b^2 ))/(4a^3 b^3 )) so answer for given problem a=2 b=3 =((π(4+9))/(4×8×27))=((13π)/(864))](Q51736.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} {xdx}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {tan}^{\mathrm{2}} {x}} \\ $$$$\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left({tanx}\right)}{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +{tan}^{\mathrm{2}} {x}} \\ $$$$\frac{\mathrm{1}}{{b}^{\mathrm{2}} }×\frac{\mathrm{1}}{\left(\frac{{a}}{{b}}\right)}\mid{tan}^{−\mathrm{1}} \left(\frac{{tanx}}{\frac{{a}}{{b}}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{{ab}}\left[{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{\pi}{\mathrm{2}}}{\frac{{a}}{{b}}}\right)−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{0}}{\frac{{a}}{{b}}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{{ab}}×{tan}^{−\mathrm{1}} \left(\infty\right)=\frac{\mathrm{1}}{{ab}}×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}{ab}} \\ $$$$ \\ $$$${solving}\:{method}−\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)}=\frac{\pi}{\mathrm{2}{ab}} \\ $$$${diferentiate}\:{both}\:{side}\:{w}.{r}.{t}\:{a} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\partial}{\partial{a}}\left[\frac{}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)}\right]{dx}=\frac{\pi}{\mathrm{2}{b}}×\frac{−\mathrm{1}}{{a}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{−\mathrm{1}×\mathrm{2}{acos}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx}=\frac{−\pi}{\mathrm{2}{a}^{\mathrm{2}} {b}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} {xdx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{4}{a}^{\mathrm{3}} {b}}.....{eqn}\:\:{p} \\ $$$${again}\:{diffdrentiate}\:{w}.{r}.{t}\:{b} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{−\mathrm{2}{bsin}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx}=\frac{−\pi}{\mathrm{2}{ab}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }=\frac{\pi}{\mathrm{4}{ab}^{\mathrm{3}} }.....{eqn}\:{q} \\ $$$${add}\:{eqn}\:{p}\:{and}\:{q} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{4}{ab}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)=\frac{\pi\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\mathrm{4}{a}^{\mathrm{3}} {b}^{\mathrm{3}} } \\ $$$${so}\:{answer} \\ $$$${for}\:{given}\:{problem}\:{a}=\mathrm{2}\:\:\:{b}=\mathrm{3} \\ $$$$=\frac{\pi\left(\mathrm{4}+\mathrm{9}\right)}{\mathrm{4}×\mathrm{8}×\mathrm{27}}=\frac{\mathrm{13}\pi}{\mathrm{864}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 30/Dec/18
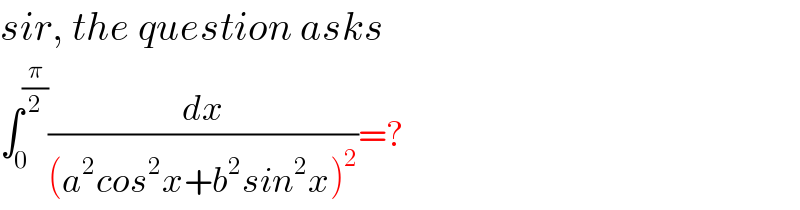
$${sir},\:{the}\:{question}\:{asks}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }=? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18

$${ok}... \\ $$$${let}\:{me}\:{solve}... \\ $$
Commented by mr W last updated on 30/Dec/18

$${yes},\:{you}\:{can}! \\ $$
Commented by mr W last updated on 30/Dec/18
$${very}\:{nice}\:{method}\:{sir}! \\ $$
Commented by Tinkutara last updated on 30/Dec/18
Can we differentiate like this w.r.t any variable?
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18

$${yes}... \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18

$${ok}\:{i}\:{am}\:{solving}\:{the}\:{problem}\:{in}\:{another}\:{method} \\ $$$${and}\:{upload}\:{problems}\:{with}\:{solution}\:{similar}\:{method} \\ $$$${of}\:{method}\:\mathrm{1} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18

$${thank}\:{you}\:{sir}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18
$${thank}\:{you}\:{for}\:{excellent}\:{post}... \\ $$
Commented by Tinkutara last updated on 30/Dec/18
Thank you very much Sir! I got the answer. ��������
Commented by afachri last updated on 30/Dec/18

$$\mathrm{i}\:\mathrm{like}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{above}\:\mathrm{Mr}\:\mathrm{Tanmay}.\: \\ $$$$\mathrm{i}\:\mathrm{save}\:\mathrm{it}\:\mathrm{to}\:\mathrm{observe}\:\:\mathrm{the}\:\mathrm{steps}.\:\mathrm{amazing} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Dec/18
![method 2 ∫_0 ^(π/2) (dx/((a^2 cos^2 x+b^2 sin^2 x)^2 )) ∫_0 ^(π/2) ((sec^4 xdx)/(b^4 [((a/b))^2 +tan^2 x]^2 )) now put tanx=(a/b)tank sec^2 xdx=(a/b)sec^2 kdk ∫_0 ^(π/2) (((1+(a^2 /b^2 )tan^2 k)×(a/b)sec^2 kdk)/(b^4 [((a/b))^2 +((a/b))^2 tan^2 k]^2 )) (a/b^3 )×(1/b^4 )∫_0 ^(π/2) (((b^2 +a^2 tan^2 k)sec^2 kdk)/(((a/b))^4 sec^4 k)) (a/b^7 )×(b^4 /a^4 )∫_0 ^(π/2) ((b^2 /(sec^2 k))+((a^2 tan^2 k)/(sec^2 k)))dk =(1/(a^3 b^3 ))∫_0 ^(π/2) (b^2 cos^2 k+a^2 sin^2 k)dk (1/(a^3 b^3 ))×(1/2)∫_0 ^(π/2) b^2 (1+cos2k)+a^2 (1−cos2k)dk (1/(2a^3 b^3 ))[∣b^2 (k+((sin2k)/2))+a^2 (k−((sin2k)/2))∣_0 ^(π/2) ] (1/(2a^3 b^3 ))[b^2 ((π/2)+((sinπ)/2))+a^2 ((π/2)−((sinπ)/2))] =(1/(2a^3 b^3 ))[(π/2)(a^2 +b^2 )] [sinπ=0] =((π(a^2 +b^2 ))/(4a^3 b^3 ))=((π(2^2 +3^2 ))/(4×8×27))=((13π)/(864))](Q51767.png)
$${method}\:\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{4}} {xdx}}{{b}^{\mathrm{4}} \left[\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +{tan}^{\mathrm{2}} {x}\right]^{\mathrm{2}} } \\ $$$${now}\:{put}\:{tanx}=\frac{{a}}{{b}}{tank} \\ $$$${sec}^{\mathrm{2}} {xdx}=\frac{{a}}{{b}}{sec}^{\mathrm{2}} {kdk} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} {k}\right)×\frac{{a}}{{b}}{sec}^{\mathrm{2}} {kdk}}{{b}^{\mathrm{4}} \left[\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} {tan}^{\mathrm{2}} {k}\right]^{\mathrm{2}} } \\ $$$$\frac{{a}}{{b}^{\mathrm{3}} }×\frac{\mathrm{1}}{{b}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} {tan}^{\mathrm{2}} {k}\right){sec}^{\mathrm{2}} {kdk}}{\left(\frac{{a}}{{b}}\right)^{\mathrm{4}} {sec}^{\mathrm{4}} {k}} \\ $$$$\frac{{a}}{{b}^{\mathrm{7}} }×\frac{{b}^{\mathrm{4}} }{{a}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{{b}^{\mathrm{2}} }{{sec}^{\mathrm{2}} {k}}+\frac{{a}^{\mathrm{2}} {tan}^{\mathrm{2}} {k}}{{sec}^{\mathrm{2}} {k}}\right){dk} \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{3}} {b}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({b}^{\mathrm{2}} {cos}^{\mathrm{2}} {k}+{a}^{\mathrm{2}} {sin}^{\mathrm{2}} {k}\right){dk} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{3}} {b}^{\mathrm{3}} }×\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {b}^{\mathrm{2}} \left(\mathrm{1}+{cos}\mathrm{2}{k}\right)+{a}^{\mathrm{2}} \left(\mathrm{1}−{cos}\mathrm{2}{k}\right){dk} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{3}} {b}^{\mathrm{3}} }\left[\mid{b}^{\mathrm{2}} \left({k}+\frac{{sin}\mathrm{2}{k}}{\mathrm{2}}\right)+{a}^{\mathrm{2}} \left({k}−\frac{{sin}\mathrm{2}{k}}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{3}} {b}^{\mathrm{3}} }\left[{b}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}+\frac{{sin}\pi}{\mathrm{2}}\right)+{a}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−\frac{{sin}\pi}{\mathrm{2}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{3}} {b}^{\mathrm{3}} }\left[\frac{\pi}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\right]\:\:\:\:\:\left[{sin}\pi=\mathrm{0}\right] \\ $$$$=\frac{\pi\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\mathrm{4}{a}^{\mathrm{3}} {b}^{\mathrm{3}} }=\frac{\pi\left(\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)}{\mathrm{4}×\mathrm{8}×\mathrm{27}}=\frac{\mathrm{13}\pi}{\mathrm{864}} \\ $$$$ \\ $$
