
Previous in Differential Equation Next in Differential Equation
Question Number 51710 by sinx last updated on 29/Dec/18
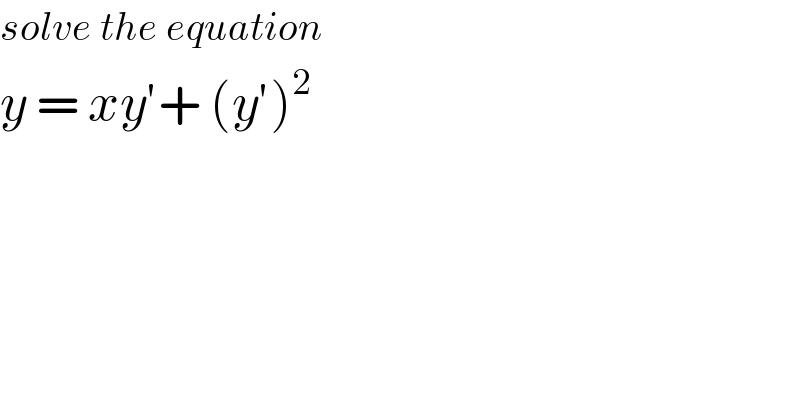
$${solve}\:{the}\:{equation} \\ $$$${y}\:=\:{xy}'+\:\left({y}'\right)^{\mathrm{2}} \\ $$
Answered by Abdulhafeez Abu qatada last updated on 30/Dec/18
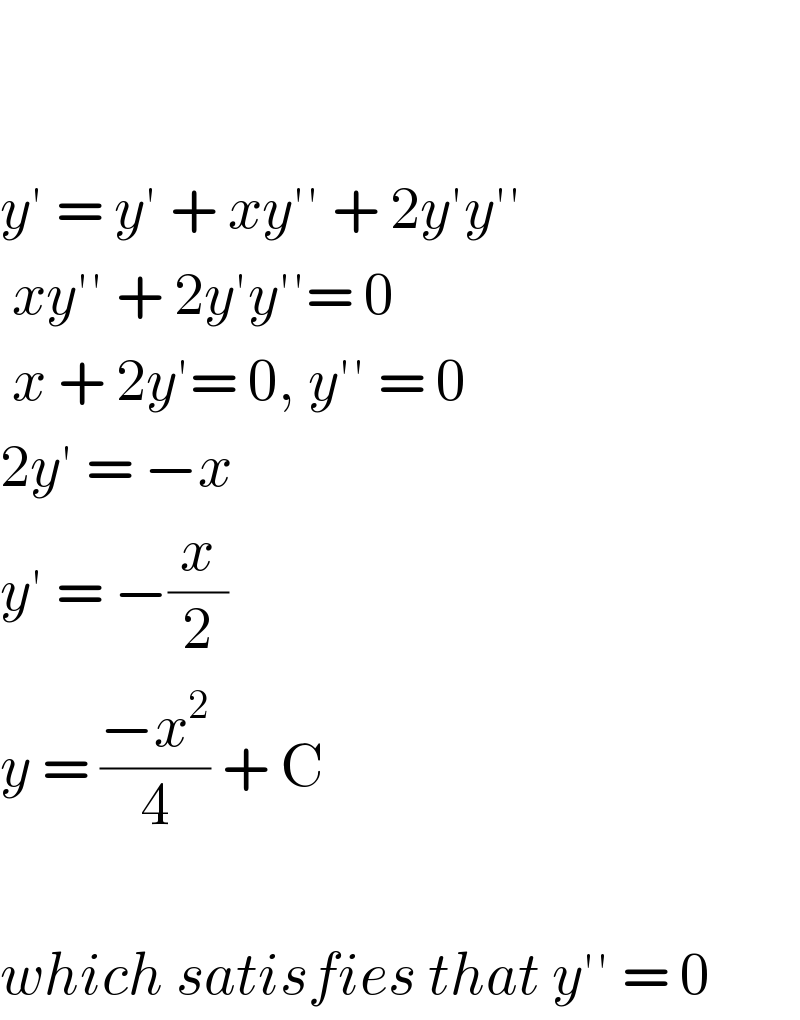
$$ \\ $$$$ \\ $$$${y}'\:=\:{y}'\:+\:{xy}''\:+\:\mathrm{2}{y}'{y}'' \\ $$$$\:{xy}''\:+\:\mathrm{2}{y}'{y}''=\:\mathrm{0} \\ $$$$\:{x}\:+\:\mathrm{2}{y}'=\:\mathrm{0},\:{y}''\:=\:\mathrm{0} \\ $$$$\mathrm{2}{y}'\:=\:−{x} \\ $$$${y}'\:=\:−\frac{{x}}{\mathrm{2}} \\ $$$${y}\:=\:\frac{−{x}^{\mathrm{2}} }{\mathrm{4}}\:+\:\mathrm{C} \\ $$$$ \\ $$$${which}\:{satisfies}\:{that}\:{y}''\:=\:\mathrm{0} \\ $$
