
Previous in Differential Equation Next in Differential Equation
Question Number 51494 by Tawa1 last updated on 27/Dec/18
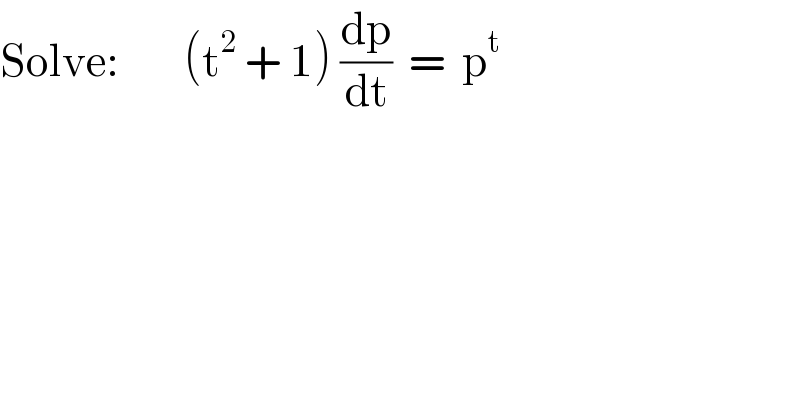
$$\mathrm{Solve}:\:\:\:\:\:\:\:\:\left(\mathrm{t}^{\mathrm{2}} \:+\:\mathrm{1}\right)\:\frac{\mathrm{dp}}{\mathrm{dt}}\:\:=\:\:\mathrm{p}^{\mathrm{t}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Dec/18
![(t^2 +1)(d^2 p/dt^2 )+(dp/dt)×2t=(d/dt)(p^t ) y=p^t lny=tlnp (1/y)(dy/dt)=(t/p)(dp/dt)+lnp (dy/dt)=y[(t/p)(dp/dt)+lnp] unique question...force the sleeping cell of brain to wake up...searching way to solve...](Q51509.png)
$$\left({t}^{\mathrm{2}} +\mathrm{1}\right)\frac{{d}^{\mathrm{2}} {p}}{{dt}^{\mathrm{2}} }+\frac{{dp}}{{dt}}×\mathrm{2}{t}=\frac{{d}}{{dt}}\left({p}^{{t}} \right) \\ $$$${y}={p}^{{t}} \\ $$$${lny}={tlnp} \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dt}}=\frac{{t}}{{p}}\frac{{dp}}{{dt}}+{lnp} \\ $$$$\frac{{dy}}{{dt}}={y}\left[\frac{{t}}{{p}}\frac{{dp}}{{dt}}+{lnp}\right] \\ $$$${unique}\:{question}...{force}\:{the}\:{sleeping}\:{cell}\:{of}\:{brain} \\ $$$${to}\:{wake}\:{up}...{searching}\:{way}\:{to}\:{solve}... \\ $$
Commented by Tawa1 last updated on 27/Dec/18

$$\mathrm{I}\:\mathrm{will}\:\mathrm{wait}\:\mathrm{sir},\:\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
