
Previous in Relation and Functions Next in Relation and Functions
Question Number 62777 by James Bryan Botshabelo last updated on 25/Jun/19
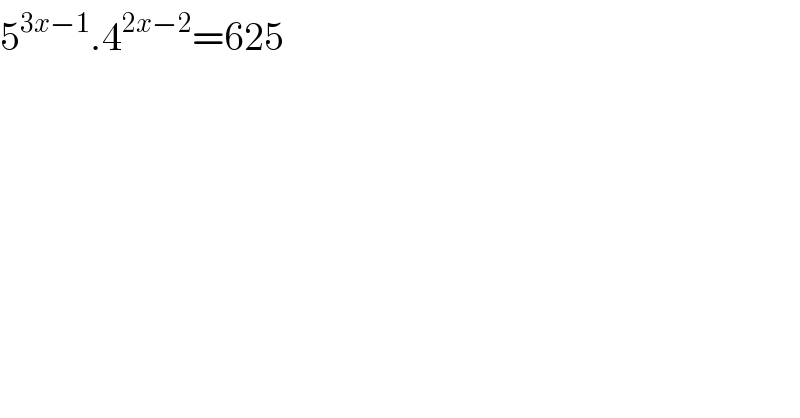
$$\mathrm{5}^{\mathrm{3}{x}−\mathrm{1}} .\mathrm{4}^{\mathrm{2}{x}−\mathrm{2}} =\mathrm{625} \\ $$
Commented by kaivan.ahmadi last updated on 25/Jun/19
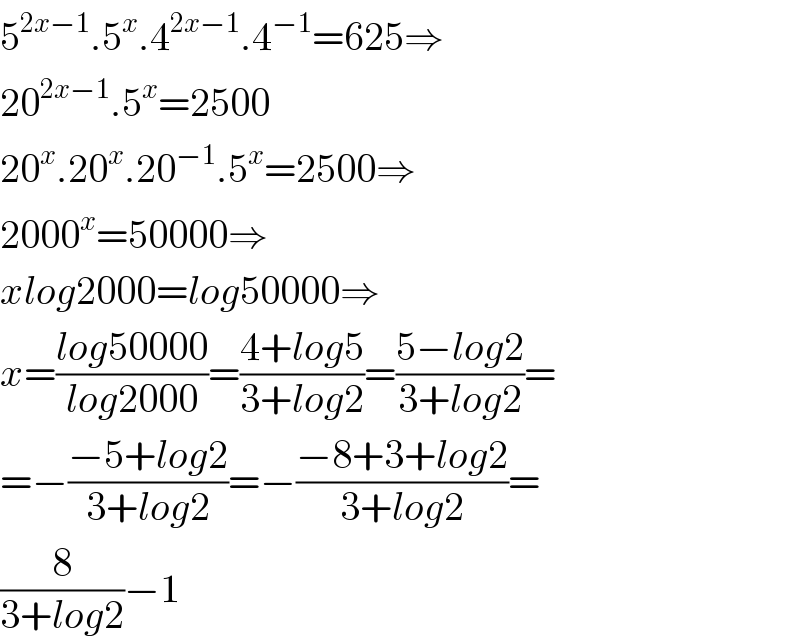
$$\mathrm{5}^{\mathrm{2}{x}−\mathrm{1}} .\mathrm{5}^{{x}} .\mathrm{4}^{\mathrm{2}{x}−\mathrm{1}} .\mathrm{4}^{−\mathrm{1}} =\mathrm{625}\Rightarrow \\ $$$$\mathrm{20}^{\mathrm{2}{x}−\mathrm{1}} .\mathrm{5}^{{x}} =\mathrm{2500} \\ $$$$\mathrm{20}^{{x}} .\mathrm{20}^{{x}} .\mathrm{20}^{−\mathrm{1}} .\mathrm{5}^{{x}} =\mathrm{2500}\Rightarrow \\ $$$$\mathrm{2000}^{{x}} =\mathrm{50000}\Rightarrow \\ $$$${xlog}\mathrm{2000}={log}\mathrm{50000}\Rightarrow \\ $$$${x}=\frac{{log}\mathrm{50000}}{{log}\mathrm{2000}}=\frac{\mathrm{4}+{log}\mathrm{5}}{\mathrm{3}+{log}\mathrm{2}}=\frac{\mathrm{5}−{log}\mathrm{2}}{\mathrm{3}+{log}\mathrm{2}}= \\ $$$$=−\frac{−\mathrm{5}+{log}\mathrm{2}}{\mathrm{3}+{log}\mathrm{2}}=−\frac{−\mathrm{8}+\mathrm{3}+{log}\mathrm{2}}{\mathrm{3}+{log}\mathrm{2}}= \\ $$$$\frac{\mathrm{8}}{\mathrm{3}+{log}\mathrm{2}}−\mathrm{1} \\ $$
