Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 59730 by muneshkumar last updated on 14/May/19

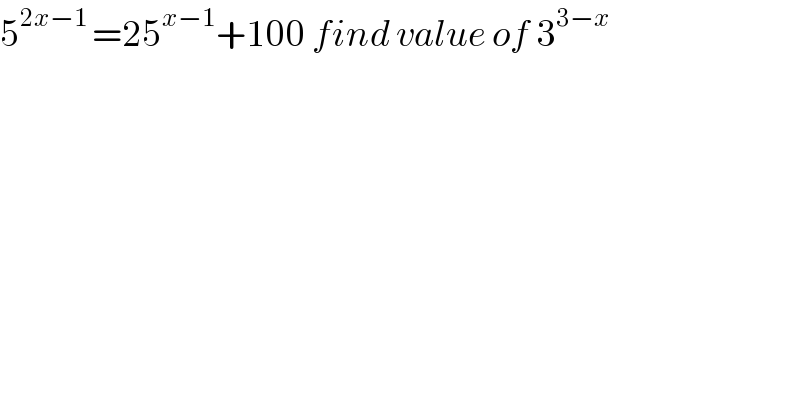
5^(2x−1 ) =25^(x−1) +100 find value of 3^(3−x)

$$\mathrm{5}^{\mathrm{2}{x}−\mathrm{1}\:} =\mathrm{25}^{{x}−\mathrm{1}} +\mathrm{100}\:{find}\:{value}\:{of}\:\mathrm{3}^{\mathrm{3}−{x}} \\ $$

Answered by tanmay last updated on 14/May/19

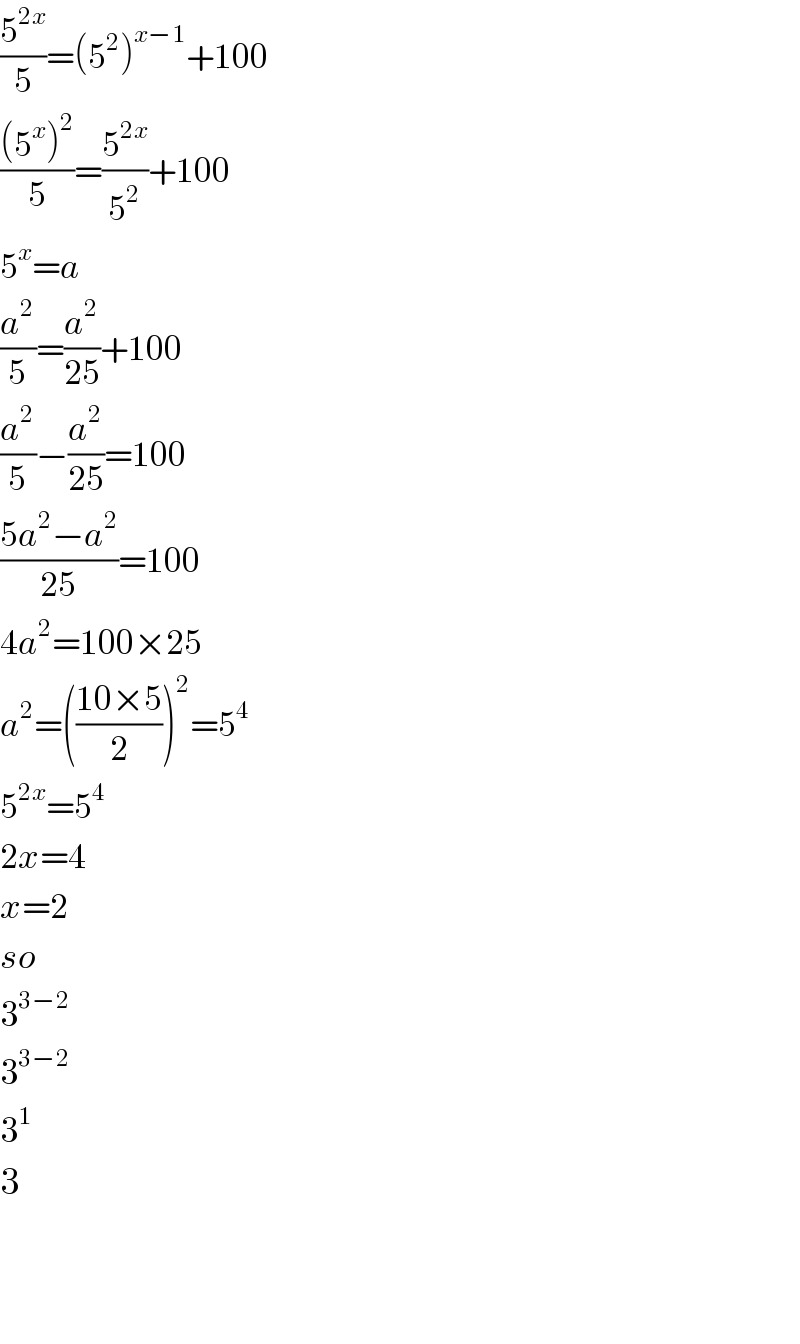
(5^(2x) /5)=(5^2 )^(x−1) +100 (((5^x )^2 )/5)=(5^(2x) /5^2 )+100 5^x =a (a^2 /5)=(a^2 /(25))+100 (a^2 /5)−(a^2 /(25))=100 ((5a^2 −a^2 )/(25))=100 4a^2 =100×25 a^2 =(((10×5)/2))^2 =5^4 5^(2x) =5^4 2x=4 x=2 so 3^(3−2) 3^(3−2) 3^1 3

$$\frac{\mathrm{5}^{\mathrm{2}{x}} }{\mathrm{5}}=\left(\mathrm{5}^{\mathrm{2}} \right)^{{x}−\mathrm{1}} +\mathrm{100} \\ $$$$\frac{\left(\mathrm{5}^{{x}} \right)^{\mathrm{2}} }{\mathrm{5}}=\frac{\mathrm{5}^{\mathrm{2}{x}} }{\mathrm{5}^{\mathrm{2}} }+\mathrm{100} \\ $$$$\mathrm{5}^{{x}} ={a} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{5}}=\frac{{a}^{\mathrm{2}} }{\mathrm{25}}+\mathrm{100} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{5}}−\frac{{a}^{\mathrm{2}} }{\mathrm{25}}=\mathrm{100} \\ $$$$\frac{\mathrm{5}{a}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{25}}=\mathrm{100} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} =\mathrm{100}×\mathrm{25} \\ $$$${a}^{\mathrm{2}} =\left(\frac{\mathrm{10}×\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{4}} \\ $$$$\mathrm{5}^{\mathrm{2}{x}} =\mathrm{5}^{\mathrm{4}} \\ $$$$\mathrm{2}{x}=\mathrm{4} \\ $$$${x}=\mathrm{2} \\ $$$${so} \\ $$$$\mathrm{3}^{\mathrm{3}−\mathrm{2}} \\ $$$$\mathrm{3}^{\mathrm{3}−\mathrm{2}} \\ $$$$\mathrm{3}^{\mathrm{1}} \\ $$$$\mathrm{3} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com