
Question Number 160179 by cortano last updated on 25/Nov/21
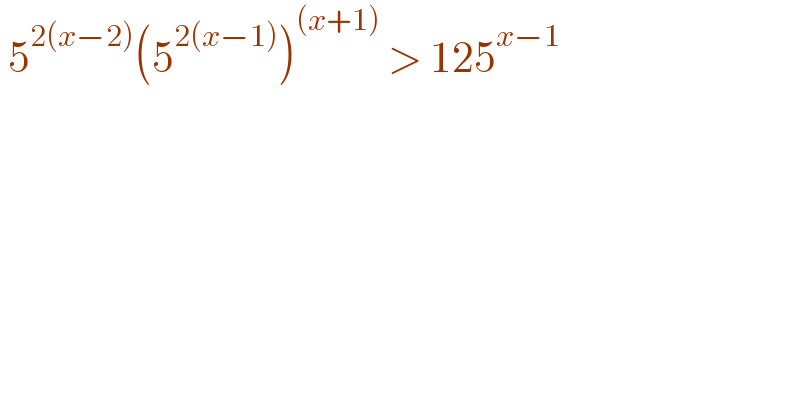
$$\:\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{2}\right)} \left(\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{1}\right)} \right)^{\left({x}+\mathrm{1}\right)} \:>\:\mathrm{125}^{{x}−\mathrm{1}} \\ $$
Commented by yeti123 last updated on 25/Nov/21
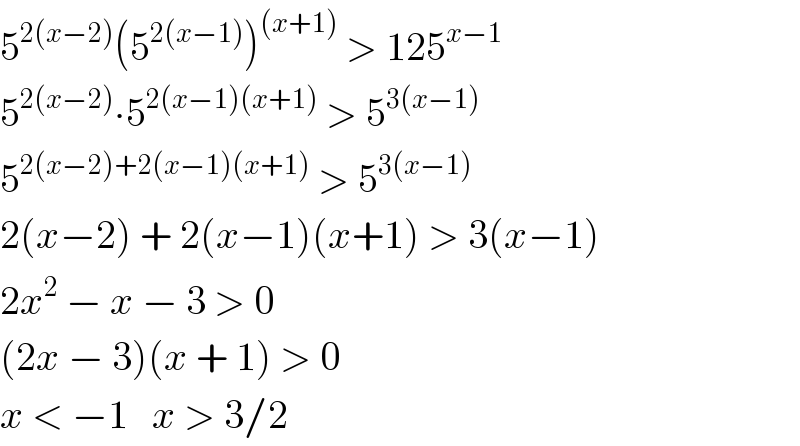
$$\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{2}\right)} \left(\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{1}\right)} \right)^{\left({x}+\mathrm{1}\right)} \:>\:\mathrm{125}^{{x}−\mathrm{1}} \\ $$$$\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{2}\right)} \centerdot\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)} \:>\:\mathrm{5}^{\mathrm{3}\left({x}−\mathrm{1}\right)} \\ $$$$\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{2}\right)+\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)} \:>\:\mathrm{5}^{\mathrm{3}\left({x}−\mathrm{1}\right)} \\ $$$$\mathrm{2}\left({x}−\mathrm{2}\right)\:+\:\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\:>\:\mathrm{3}\left({x}−\mathrm{1}\right) \\ $$$$\mathrm{2}{x}^{\mathrm{2}} \:−\:{x}\:−\:\mathrm{3}\:>\:\mathrm{0} \\ $$$$\left(\mathrm{2}{x}\:−\:\mathrm{3}\right)\left({x}\:+\:\mathrm{1}\right)\:>\:\mathrm{0} \\ $$$${x}\:<\:−\mathrm{1}\:\:\:{x}\:>\:\mathrm{3}/\mathrm{2} \\ $$
Commented by blackmamba last updated on 25/Nov/21
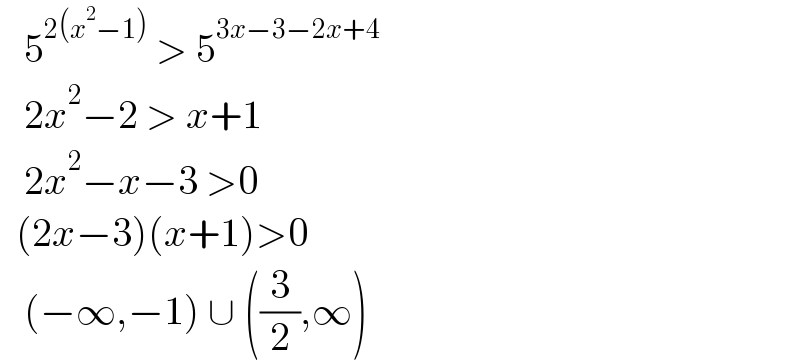
$$\:\:\:\mathrm{5}^{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)} \:>\:\mathrm{5}^{\mathrm{3}{x}−\mathrm{3}−\mathrm{2}{x}+\mathrm{4}} \\ $$$$\:\:\:\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}\:>\:{x}+\mathrm{1} \\ $$$$\:\:\:\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{3}\:>\mathrm{0} \\ $$$$\:\:\left(\mathrm{2}{x}−\mathrm{3}\right)\left({x}+\mathrm{1}\right)>\mathrm{0} \\ $$$$\:\:\:\left(−\infty,−\mathrm{1}\right)\:\cup\:\left(\frac{\mathrm{3}}{\mathrm{2}},\infty\right) \\ $$
Answered by Rasheed.Sindhi last updated on 25/Nov/21
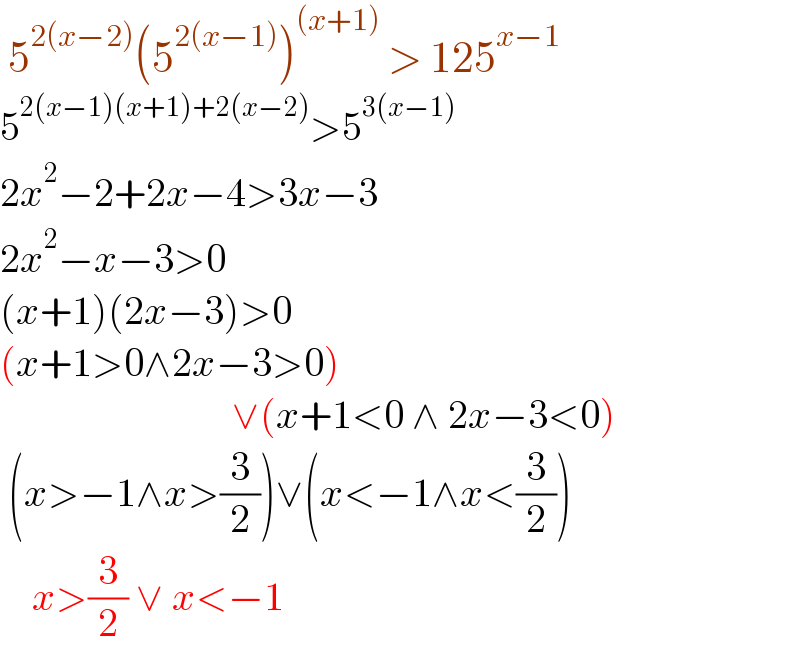
$$\:\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{2}\right)} \left(\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{1}\right)} \right)^{\left({x}+\mathrm{1}\right)} \:>\:\mathrm{125}^{{x}−\mathrm{1}} \\ $$$$\mathrm{5}^{\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)+\mathrm{2}\left({x}−\mathrm{2}\right)} >\mathrm{5}^{\mathrm{3}\left({x}−\mathrm{1}\right)} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}+\mathrm{2}{x}−\mathrm{4}>\mathrm{3}{x}−\mathrm{3} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{3}>\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{3}\right)>\mathrm{0} \\ $$$$\left({x}+\mathrm{1}>\mathrm{0}\wedge\mathrm{2}{x}−\mathrm{3}>\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee\left({x}+\mathrm{1}<\mathrm{0}\:\wedge\:\mathrm{2}{x}−\mathrm{3}<\mathrm{0}\right) \\ $$$$\:\left({x}>−\mathrm{1}\wedge{x}>\frac{\mathrm{3}}{\mathrm{2}}\right)\vee\left({x}<−\mathrm{1}\wedge{x}<\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:{x}>\frac{\mathrm{3}}{\mathrm{2}}\:\vee\:{x}<−\mathrm{1} \\ $$
