Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85601 by sahnaz last updated on 23/Mar/20

∫((4u)/(4u^2 −4u+1))du

$$\int\frac{\mathrm{4u}}{\mathrm{4u}^{\mathrm{2}} −\mathrm{4u}+\mathrm{1}}\mathrm{du} \\ $$

Commented by Tony Lin last updated on 23/Mar/20

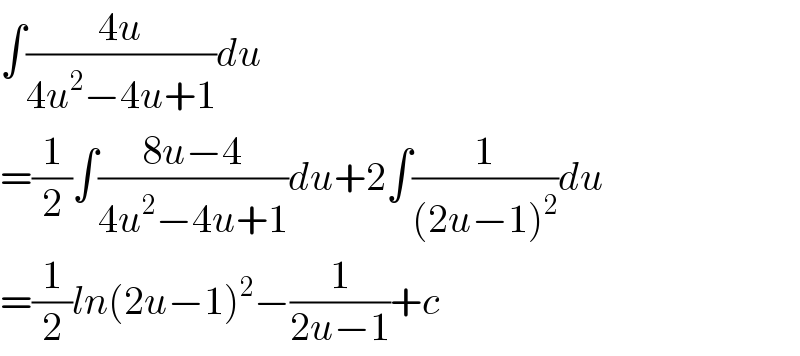
∫((4u)/(4u^2 −4u+1))du =(1/2)∫((8u−4)/(4u^2 −4u+1))du+2∫(1/((2u−1)^2 ))du =(1/2)ln(2u−1)^2 −(1/(2u−1))+c

$$\int\frac{\mathrm{4}{u}}{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{8}{u}−\mathrm{4}}{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}}{du}+\mathrm{2}\int\frac{\mathrm{1}}{\left(\mathrm{2}{u}−\mathrm{1}\right)^{\mathrm{2}} }{du}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}{u}−\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{u}−\mathrm{1}}+{c} \\ $$

Commented by mathmax by abdo last updated on 23/Mar/20

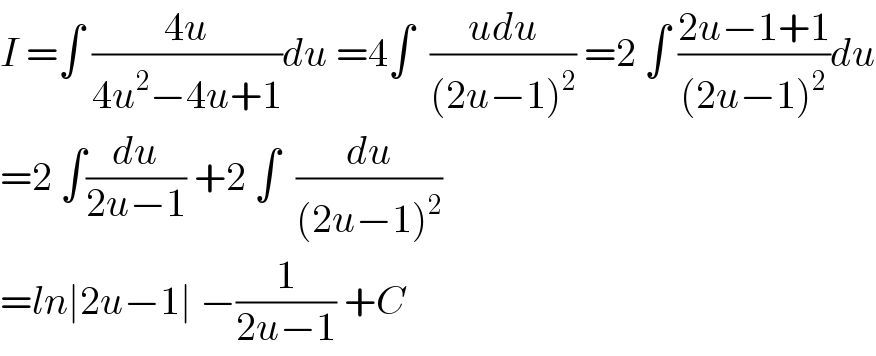
I =∫ ((4u)/(4u^2 −4u+1))du =4∫ ((udu)/((2u−1)^2 )) =2 ∫ ((2u−1+1)/((2u−1)^2 ))du =2 ∫(du/(2u−1)) +2 ∫ (du/((2u−1)^2 )) =ln∣2u−1∣ −(1/(2u−1)) +C

$${I}\:=\int\:\frac{\mathrm{4}{u}}{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{1}}{du}\:=\mathrm{4}\int\:\:\frac{{udu}}{\left(\mathrm{2}{u}−\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{2}\:\int\:\frac{\mathrm{2}{u}−\mathrm{1}+\mathrm{1}}{\left(\mathrm{2}{u}−\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$=\mathrm{2}\:\int\frac{{du}}{\mathrm{2}{u}−\mathrm{1}}\:+\mathrm{2}\:\int\:\:\frac{{du}}{\left(\mathrm{2}{u}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$={ln}\mid\mathrm{2}{u}−\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{2}{u}−\mathrm{1}}\:+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com