
Question Number 49806 by maxmathsup by imad last updated on 10/Dec/18
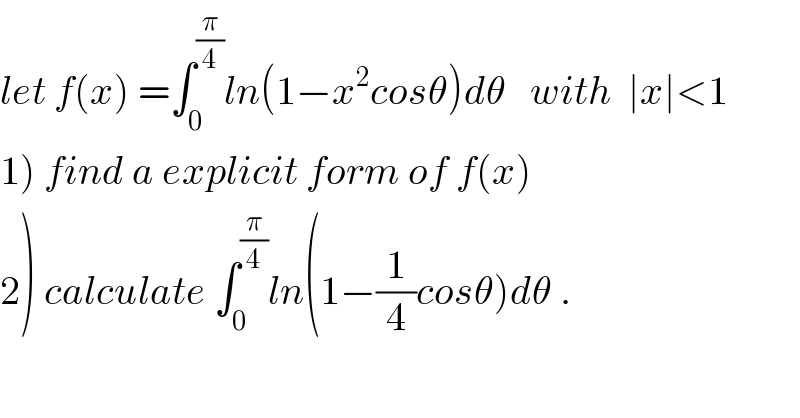
$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}−{x}^{\mathrm{2}} {cos}\theta\right){d}\theta\:\:\:{with}\:\:\mid{x}\mid<\mathrm{1} \\ $$ $$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{cos}\theta\right){d}\theta\:. \\ $$
Commented byAbdo msup. last updated on 12/Dec/18

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{−\mathrm{2}{xcos}\theta}{\mathrm{1}−{x}^{\mathrm{2}} {cos}\theta}\:{d}\theta \\ $$ $$=\frac{\mathrm{2}}{{x}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{\mathrm{1}−{x}^{\mathrm{2}} {cos}\theta\:−\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} {cos}\theta}\:{d}\theta \\ $$ $$=\frac{\pi}{\mathrm{2}{x}}\:−\frac{\mathrm{2}}{{x}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{d}\theta}{\mathrm{1}−{x}^{\mathrm{2}} {cos}\theta}\:{let}\:{find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{d}\theta}{\mathrm{1}−{x}^{\mathrm{2}} {cos}\theta} \\ $$ $${changement}\:\:{tan}\left(\frac{\theta}{\mathrm{2}}\right)={t}\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{d}\theta}{\mathrm{1}−{x}^{\mathrm{2}} {cos}\theta}\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} \frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$ $$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:−{x}^{\mathrm{2}} \:+{x}^{\mathrm{2}} {t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}−{x}^{\mathrm{2}} \:+\left(\mathrm{1}+{x}^{\mathrm{2}} \right){t}^{\mathrm{2}} } \\ $$ $$=\frac{\mathrm{2}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\frac{{dt}}{\mathrm{1}+\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }{t}^{\mathrm{2}} }{let}\:{suppose}\:\mid{x}\mid<\mathrm{1} \\ $$ $$=_{\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }{t}}={u}} \:\:\:\:\frac{\mathrm{2}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\sqrt{\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}{du} \\ $$ $$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:{arctan}\left\{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\right\}\:\Rightarrow \\ $$ $${f}^{'} \left({x}\right)=\:\frac{\pi}{\mathrm{2}{x}}\:−\frac{\mathrm{1}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:{arctan}\left\{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\right\}\:\Rightarrow \\ $$ $${f}\left({x}\right)=\frac{\pi}{\mathrm{2}}{ln}\mid{x}\mid\:−\int_{\mathrm{1}} ^{{x}} \:\frac{\mathrm{1}}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}\:{arctan}\left\{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }}\right\}\:+\lambda \\ $$
