
Previous in Relation and Functions Next in Relation and Functions
Question Number 49804 by maxmathsup by imad last updated on 10/Dec/18
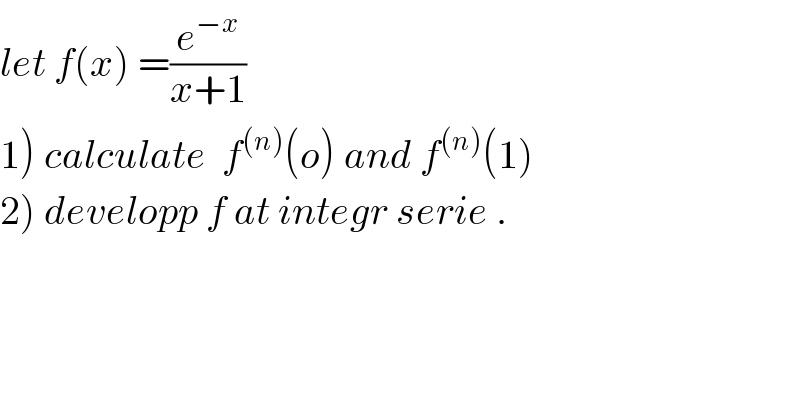
$${let}\:{f}\left({x}\right)\:=\frac{{e}^{−{x}} }{{x}+\mathrm{1}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\:{f}^{\left({n}\right)} \left({o}\right)\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}\:. \\ $$
Commented by Abdo msup. last updated on 11/Dec/18
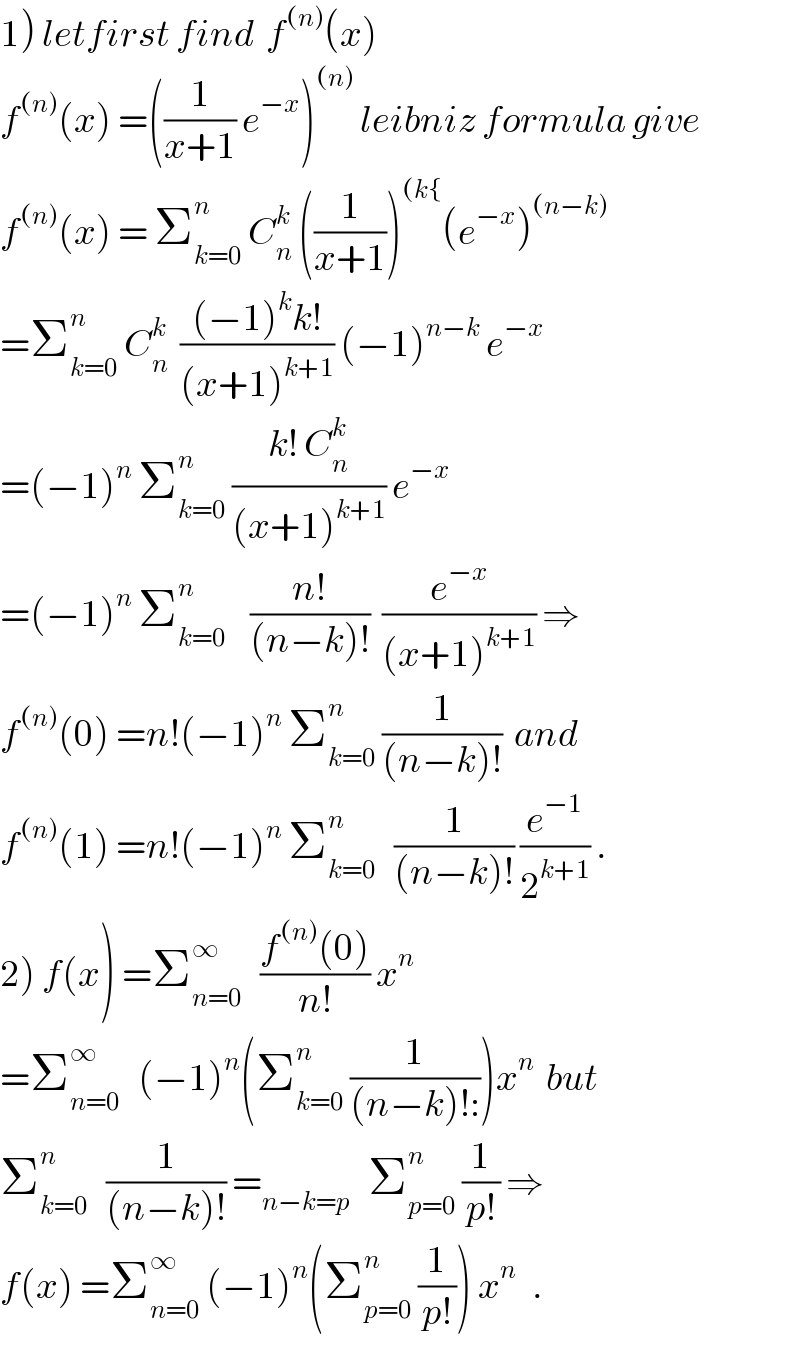
$$\left.\mathrm{1}\right)\:{letfirst}\:{find}\:\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\:{e}^{−{x}} \right)^{\left({n}\right)} \:{leibniz}\:{formula}\:{give} \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)^{\left({k}\left\{\right.\right.} \left({e}^{−{x}} \right)^{\left({n}−{k}\right)} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} {k}!}{\left({x}+\mathrm{1}\right)^{{k}+\mathrm{1}} }\:\left(−\mathrm{1}\right)^{{n}−{k}} \:{e}^{−{x}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{k}!\:{C}_{{n}} ^{{k}} }{\left({x}+\mathrm{1}\right)^{{k}+\mathrm{1}} }\:{e}^{−{x}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:\:\frac{{n}!}{\left({n}−{k}\right)!}\:\:\frac{{e}^{−{x}} }{\left({x}+\mathrm{1}\right)^{{k}+\mathrm{1}} }\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:={n}!\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\left({n}−{k}\right)!}\:\:{and} \\ $$$${f}^{\left({n}\right)} \left(\mathrm{1}\right)\:={n}!\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:\frac{\mathrm{1}}{\left({n}−{k}\right)!}\:\frac{{e}^{−\mathrm{1}} }{\mathrm{2}^{{k}+\mathrm{1}} }\:. \\ $$$$\left.\mathrm{2}\right)\:{f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\left(−\mathrm{1}\right)^{{n}} \left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\left({n}−{k}\right)!:}\right){x}^{{n}} \:\:{but}\: \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:\frac{\mathrm{1}}{\left({n}−{k}\right)!}\:=_{{n}−{k}={p}} \:\:\:\sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{p}!}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \left(\sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{p}!}\right)\:{x}^{{n}\:} \:\:. \\ $$
