
Question Number 49294 by peter frank last updated on 05/Dec/18
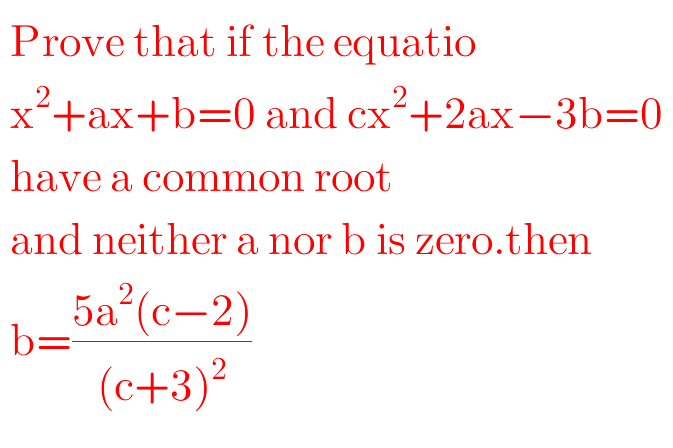
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18
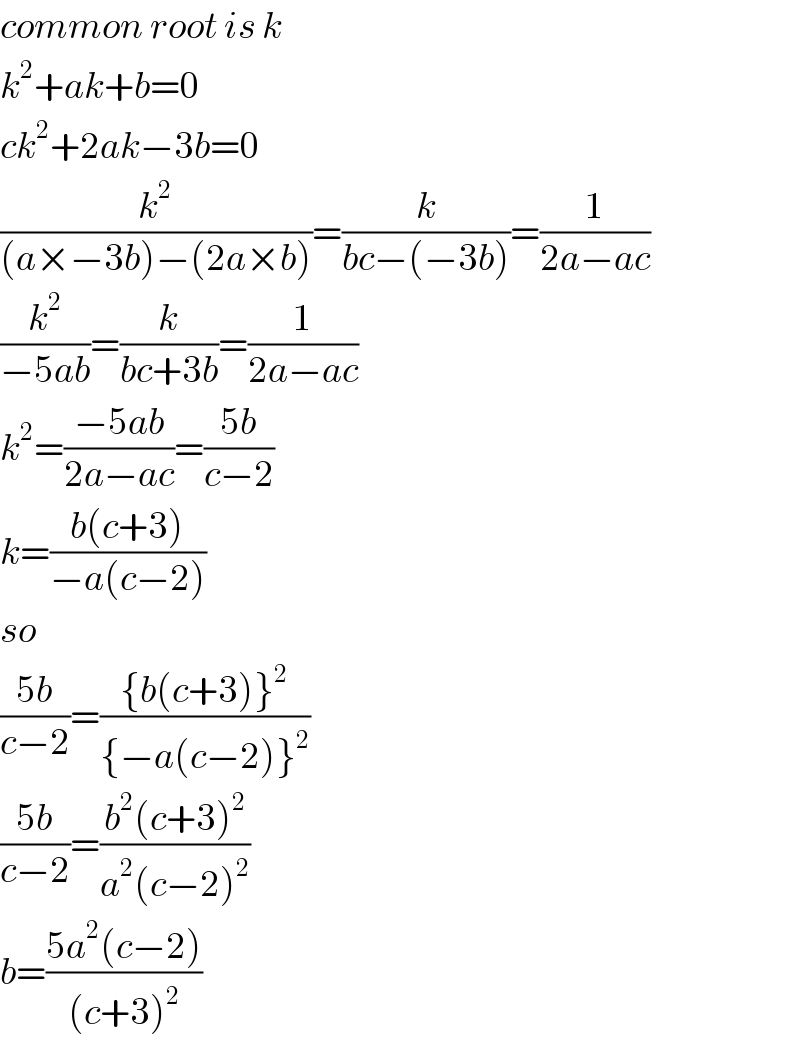
$${common}\:{root}\:{is}\:{k} \\ $$$${k}^{\mathrm{2}} +{ak}+{b}=\mathrm{0} \\ $$$${ck}^{\mathrm{2}} +\mathrm{2}{ak}−\mathrm{3}{b}=\mathrm{0} \\ $$$$\frac{{k}^{\mathrm{2}} }{\left({a}×−\mathrm{3}{b}\right)−\left(\mathrm{2}{a}×{b}\right)}=\frac{{k}}{{bc}−\left(−\mathrm{3}{b}\right)}=\frac{\mathrm{1}}{\mathrm{2}{a}−{ac}} \\ $$$$\frac{{k}^{\mathrm{2}} }{−\mathrm{5}{ab}}=\frac{{k}}{{bc}+\mathrm{3}{b}}=\frac{\mathrm{1}}{\mathrm{2}{a}−{ac}} \\ $$$${k}^{\mathrm{2}} =\frac{−\mathrm{5}{ab}}{\mathrm{2}{a}−{ac}}=\frac{\mathrm{5}{b}}{{c}−\mathrm{2}} \\ $$$${k}=\frac{{b}\left({c}+\mathrm{3}\right)}{−{a}\left({c}−\mathrm{2}\right)} \\ $$$${so} \\ $$$$\frac{\mathrm{5}{b}}{{c}−\mathrm{2}}=\frac{\left\{{b}\left({c}+\mathrm{3}\right)\right\}^{\mathrm{2}} }{\left\{−{a}\left({c}−\mathrm{2}\right)\right\}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{5}{b}}{{c}−\mathrm{2}}=\frac{{b}^{\mathrm{2}} \left({c}+\mathrm{3}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} \left({c}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${b}=\frac{\mathrm{5}{a}^{\mathrm{2}} \left({c}−\mathrm{2}\right)}{\left({c}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$
