
Question Number 49279 by Tawa1 last updated on 05/Dec/18
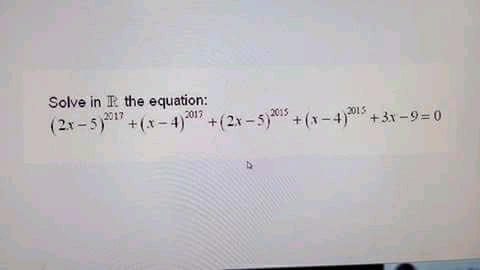
Commented by MJS last updated on 05/Dec/18

$${x}−\mathrm{4}={u} \\ $$$$\mathrm{2}{x}−\mathrm{5}={v} \\ $$$${u}^{\mathrm{2017}} +{u}^{\mathrm{2015}} +{u}=−\left({v}^{\mathrm{2017}} +{v}^{\mathrm{2015}} +{v}\right) \\ $$$$\Rightarrow\:{v}=−{u}\:\Leftrightarrow\:{u}+{v}=\mathrm{0} \\ $$$$\mathrm{3}{x}−\mathrm{9}=\mathrm{0} \\ $$$${x}=\mathrm{3} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{put} \\ $$$${u}^{{n}} +{u}^{{n}−\mathrm{2}} +{u}+{v}^{{n}} +{v}^{{n}−\mathrm{2}} +{v}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{test}\:\mathrm{for}\:{n}=\mathrm{2}{k}+\mathrm{1};\:{k}\in\mathbb{N}^{\bigstar} \:\mathrm{if} \\ $$$${u}^{\mathrm{2}{k}+\mathrm{1}} +{u}^{\mathrm{2}{k}−\mathrm{1}} +{u}+{v}^{\mathrm{2}{k}+\mathrm{1}} +{v}^{\mathrm{2}{k}−\mathrm{1}} +{v}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{got}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\mathrm{I}\:\mathrm{tested}\:\mathrm{for}\:{k}=\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\right\}\:\mathrm{and}\:\mathrm{found}\:\mathrm{no} \\ $$$$\mathrm{real}\:\mathrm{solutions}\:\mathrm{except}\:{v}=−{u} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{prove}\:\mathrm{it} \\ $$
Answered by afachri last updated on 05/Dec/18
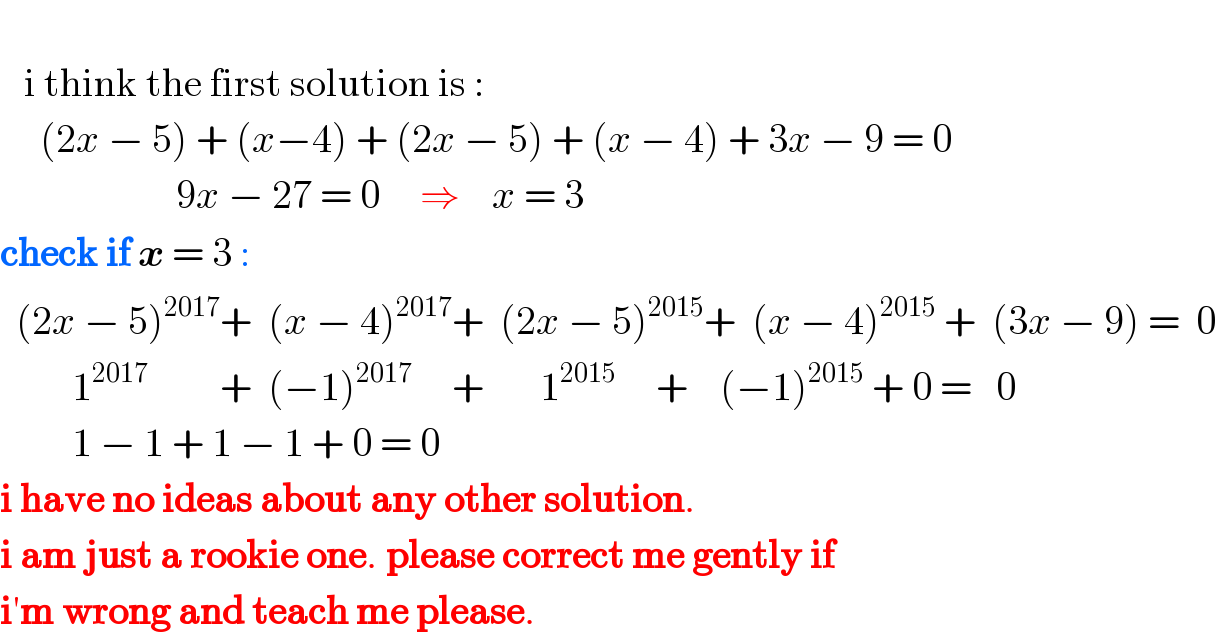
$$ \\ $$$$\:\:\:\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{first}\:\mathrm{solution}\:\mathrm{is}\::\: \\ $$$$\:\:\:\:\:\left(\mathrm{2}{x}\:−\:\mathrm{5}\right)\:+\:\left({x}−\mathrm{4}\right)\:+\:\left(\mathrm{2}{x}\:−\:\mathrm{5}\right)\:+\:\left({x}\:−\:\mathrm{4}\right)\:+\:\mathrm{3}{x}\:−\:\mathrm{9}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}{x}\:−\:\mathrm{27}\:=\:\mathrm{0}\:\:\:\:\:\Rightarrow\:\:\:\:{x}\:=\:\mathrm{3} \\ $$$$\boldsymbol{\mathrm{check}}\:\boldsymbol{\mathrm{if}}\:\boldsymbol{{x}}\:=\:\mathrm{3}\::\: \\ $$$$\:\:\left(\mathrm{2}{x}\:−\:\mathrm{5}\right)^{\mathrm{2017}} +\:\:\left({x}\:−\:\mathrm{4}\right)^{\mathrm{2017}} +\:\:\left(\mathrm{2}{x}\:−\:\mathrm{5}\right)^{\mathrm{2015}} +\:\:\left({x}\:−\:\mathrm{4}\right)^{\mathrm{2015}} \:+\:\:\left(\mathrm{3}{x}\:−\:\mathrm{9}\right)\:=\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{1}^{\mathrm{2017}} \:\:\:\:\:\:\:\:\:+\:\:\left(−\mathrm{1}\right)^{\mathrm{2017}} \:\:\:\:\:+\:\:\:\:\:\:\:\mathrm{1}^{\mathrm{2015}} \:\:\:\:\:+\:\:\:\:\left(−\mathrm{1}\right)^{\mathrm{2015}} \:+\:\mathrm{0}\:=\:\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{1}\:−\:\mathrm{1}\:+\:\mathrm{1}\:−\:\mathrm{1}\:+\:\mathrm{0}\:=\:\mathrm{0} \\ $$$$\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{no}}\:\boldsymbol{\mathrm{ideas}}\:\boldsymbol{\mathrm{about}}\:\boldsymbol{\mathrm{any}}\:\boldsymbol{\mathrm{other}}\:\boldsymbol{\mathrm{solution}}.\: \\ $$$$\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{am}}\:\boldsymbol{\mathrm{just}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{rookie}}\:\boldsymbol{\mathrm{one}}.\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{correct}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{gently}}\:\boldsymbol{\mathrm{if}}\: \\ $$$$\boldsymbol{\mathrm{i}}'\boldsymbol{\mathrm{m}}\:\boldsymbol{\mathrm{wrong}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{teach}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{please}}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18
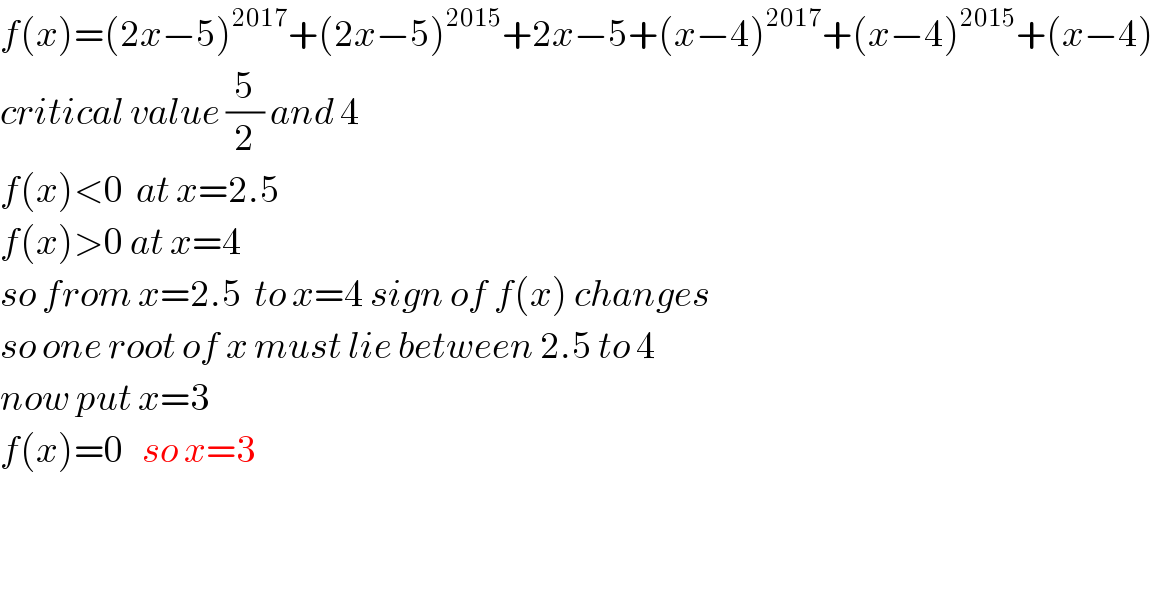
$${f}\left({x}\right)=\left(\mathrm{2}{x}−\mathrm{5}\right)^{\mathrm{2017}} +\left(\mathrm{2}{x}−\mathrm{5}\right)^{\mathrm{2015}} +\mathrm{2}{x}−\mathrm{5}+\left({x}−\mathrm{4}\right)^{\mathrm{2017}} +\left({x}−\mathrm{4}\right)^{\mathrm{2015}} +\left({x}−\mathrm{4}\right) \\ $$$${critical}\:{value}\:\frac{\mathrm{5}}{\mathrm{2}}\:{and}\:\mathrm{4} \\ $$$${f}\left({x}\right)<\mathrm{0}\:\:{at}\:{x}=\mathrm{2}.\mathrm{5} \\ $$$${f}\left({x}\right)>\mathrm{0}\:{at}\:{x}=\mathrm{4} \\ $$$${so}\:{from}\:{x}=\mathrm{2}.\mathrm{5}\:\:{to}\:{x}=\mathrm{4}\:{sign}\:{of}\:{f}\left({x}\right)\:{changes} \\ $$$${so}\:{one}\:{root}\:{of}\:{x}\:{must}\:{lie}\:{between}\:\mathrm{2}.\mathrm{5}\:{to}\:\mathrm{4} \\ $$$${now}\:{put}\:{x}=\mathrm{3} \\ $$$${f}\left({x}\right)=\mathrm{0}\:\:\:{so}\:{x}=\mathrm{3}\: \\ $$$$ \\ $$$$ \\ $$
