
Question Number 49253 by cesar.marval.larez@gmail.com last updated on 04/Dec/18
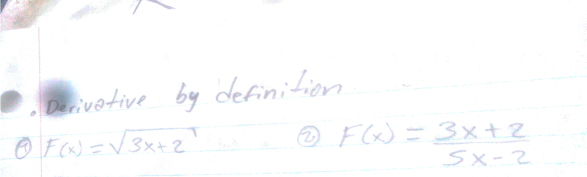
Answered by afachri last updated on 05/Dec/18
![no. 2 f′(x) = lim_(h→0) [(( (((3(x + h) + 2)/(5(x + h) − 2)) − ((3x + 2)/(5x − 2 ))) )/h)] = lim_(h→0) (1/h)( (( 3x + 3h + 2 )/(5x + 5h − 2)) − (( 3x + 2)/(5x − 2)) ) = lim_(h→0) (1/h) ((( (5x−2)(3x + 3h + 2) − (3x+2)(5x + 5h − 2) )/( (5x + 5h − 2) (5x − 2) ))) = lim_(h→0) (1/h) ((( 16h)/( (5x + 5h −2)(5x−2)))) = lim_(h→0) ((( 16)/((5x + 5h −2)(5x − 2)))) ∙∙∙∙put h = 0 in the equation, so : = lim_(h→0) ((( 16)/( (5x + 5(0) − 2)(5x − 2)))) = (( 16)/( (5x − 2)(5x − 2))) conclusion : (d/dx)((( 3x + 2 )/(5x − 2))) = (( 16)/( (5x − 2)^2 ))](Q49270.png)
$$\boldsymbol{\mathrm{no}}.\:\mathrm{2} \\ $$$$\boldsymbol{{f}}'\left({x}\right)\:=\:\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left[\frac{\:\:\:\:\:\left(\frac{\mathrm{3}\left({x}\:+\:{h}\right)\:+\:\mathrm{2}}{\mathrm{5}\left({x}\:+\:{h}\right)\:−\:\mathrm{2}}\:\:−\:\:\frac{\mathrm{3}{x}\:+\:\mathrm{2}}{\mathrm{5}{x}\:−\:\mathrm{2}\:}\right)\:\:\:\:}{{h}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}}{{h}}\left(\:\frac{\:\mathrm{3}{x}\:+\:\mathrm{3}{h}\:+\:\mathrm{2}\:}{\mathrm{5}{x}\:+\:\mathrm{5}{h}\:−\:\mathrm{2}}\:\:−\:\:\frac{\:\mathrm{3}{x}\:+\:\mathrm{2}}{\mathrm{5}{x}\:−\:\mathrm{2}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{{h}}\:\left(\frac{\:\left(\mathrm{5}{x}−\mathrm{2}\right)\left(\mathrm{3}{x}\:+\:\mathrm{3}{h}\:+\:\mathrm{2}\right)\:\:−\:\:\left(\mathrm{3}{x}+\mathrm{2}\right)\left(\mathrm{5}{x}\:+\:\mathrm{5}{h}\:−\:\mathrm{2}\right)\:}{\:\left(\mathrm{5}{x}\:+\:\mathrm{5}{h}\:−\:\mathrm{2}\right)\:\left(\mathrm{5}{x}\:−\:\mathrm{2}\right)\:}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\boldsymbol{{h}}}\:\left(\frac{\:\mathrm{16}\boldsymbol{{h}}}{\:\left(\mathrm{5}{x}\:+\:\mathrm{5}{h}\:−\mathrm{2}\right)\left(\mathrm{5}{x}−\mathrm{2}\right)}\right)\:\:=\:\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left(\frac{\:\mathrm{16}}{\left(\mathrm{5}{x}\:+\:\mathrm{5}\boldsymbol{{h}}\:−\mathrm{2}\right)\left(\mathrm{5}{x}\:−\:\mathrm{2}\right)}\right) \\ $$$$\centerdot\centerdot\centerdot\centerdot\boldsymbol{\mathrm{put}}\:\boldsymbol{{h}}\:=\:\mathrm{0}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equation}},\:\boldsymbol{\mathrm{so}}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left(\frac{\:\mathrm{16}}{\:\left(\mathrm{5}\boldsymbol{{x}}\:+\:\mathrm{5}\left(\mathrm{0}\right)\:−\:\mathrm{2}\right)\left(\mathrm{5}{x}\:−\:\mathrm{2}\right)}\right)\:\:=\:\:\frac{\:\mathrm{16}}{\:\left(\mathrm{5}{x}\:−\:\mathrm{2}\right)\left(\mathrm{5}{x}\:−\:\mathrm{2}\right)} \\ $$$$\boldsymbol{\mathrm{conclusion}}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left(\frac{\:\mathrm{3}\boldsymbol{{x}}\:+\:\mathrm{2}\:}{\mathrm{5}\boldsymbol{{x}}\:−\:\mathrm{2}}\right)\:=\:\:\frac{\:\mathrm{16}}{\:\left(\mathrm{5}\boldsymbol{{x}}\:−\:\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$
Answered by afachri last updated on 05/Dec/18
![no. 1 f′(x) = lim_(h→0) ((F(x + h)−F(x))/h) = lim_(h→0) (((√(3(x + h)^ +2 ))− (√(3x^ + 2 )))/h) = lim_(h→0) (((√(3(x + h)^ + 2 )) − (√(3x^ + 2 )))/h) × (((√(3(x + h)^ + 2)) + (√(3x + 2^ )) )/((√(3(x + h)^ +2 )) + (√(3x^ + 2 )))) = lim_(h→0) [((3(x + h) + 2 − (3x+2))/(h((√(3(x + h)^ + 2)) + (√(3x^ + 2)) )))] = lim_(h→0) [ ((3h)/(h((√(3(x + h)^ + 2)) + (√(3x^ + 2)))))] = lim_(h→0) (3/((√(3(x + h)^ + 2)) + (√(3x^ + 2 )) )) , put h = 0 then = lim_(h→0) (3/((√(3x^ + 2 )) + (√(3x^ + 2 )))) = (3/(2(√(3x^ + 2 )))) conclusion : (d/dx)((√(3x^ +2 ))) = (3/(2(√(3x^ + 2 ))))](Q49267.png)
$$\boldsymbol{\mathrm{no}}.\:\mathrm{1} \\ $$$$\boldsymbol{{f}}'\left({x}\right)\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{F}\left({x}\:+\:{h}\right)−{F}\left({x}\right)}{{h}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{3}\left({x}\:+\:{h}\right)^{} \:+\mathrm{2}\:}−\:\sqrt{\mathrm{3}{x}^{} \:+\:\mathrm{2}\:}}{{h}}\:\:=\:\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{3}\left({x}\:+\:{h}\right)^{} \:+\:\mathrm{2}\:}\:−\:\sqrt{\mathrm{3}{x}^{} \:+\:\mathrm{2}\:}}{{h}}\:×\:\frac{\sqrt{\mathrm{3}\left({x}\:+\:{h}\right)^{} +\:\mathrm{2}}\:+\:\sqrt{\mathrm{3}{x}\:+\:\mathrm{2}^{} }\:}{\sqrt{\mathrm{3}\left({x}\:+\:{h}\right)^{} +\mathrm{2}\:}\:+\:\sqrt{\mathrm{3}{x}^{} +\:\mathrm{2}\:}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\left[\frac{\mathrm{3}\left({x}\:+\:{h}\right)\:+\:\mathrm{2}\:−\:\left(\mathrm{3}{x}+\mathrm{2}\right)}{{h}\left(\sqrt{\mathrm{3}\left({x}\:+\:{h}\right)^{} +\:\mathrm{2}}\:\:+\:\sqrt{\mathrm{3}{x}^{} +\:\mathrm{2}}\:\right)}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\left[\:\frac{\mathrm{3}\boldsymbol{{h}}}{\boldsymbol{{h}}\left(\sqrt{\mathrm{3}\left({x}\:+\:{h}\right)^{} +\:\mathrm{2}}\:\:+\:\sqrt{\mathrm{3}{x}^{} +\:\mathrm{2}}\right)}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\mathrm{3}}{\sqrt{\mathrm{3}\left({x}\:+\:{h}\right)^{} \:+\:\mathrm{2}}\:\:+\:\sqrt{\mathrm{3}{x}^{} \:+\:\mathrm{2}\:}\:}\:\:,\:\boldsymbol{\mathrm{put}}\:\boldsymbol{{h}}\:=\:\mathrm{0}\:\boldsymbol{\mathrm{then}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{3}}{\sqrt{\mathrm{3}\boldsymbol{{x}}^{} +\:\mathrm{2}\:}\:\:+\:\:\sqrt{\mathrm{3}\boldsymbol{{x}}^{} +\:\mathrm{2}\:}}\:\:=\:\:\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{3}\boldsymbol{{x}}^{} +\:\mathrm{2}\:}} \\ $$$$\boldsymbol{\mathrm{conclusion}}\:: \\ $$$$\:\:\:\:\:\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left(\sqrt{\mathrm{3}\boldsymbol{{x}}^{} +\mathrm{2}\:}\right)\:=\:\:\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{3}\boldsymbol{{x}}^{} +\:\mathrm{2}\:}} \\ $$$$ \\ $$
