
Question Number 49169 by rahul 19 last updated on 04/Dec/18
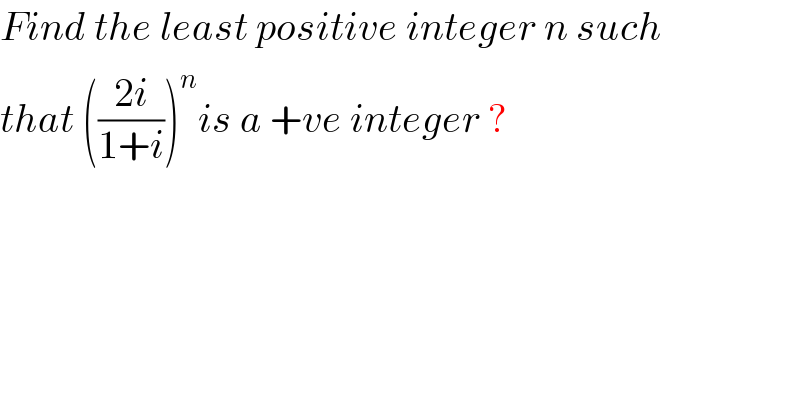
$${Find}\:{the}\:{least}\:{positive}\:{integer}\:{n}\:{such} \\ $$$${that}\:\left(\frac{\mathrm{2}{i}}{\mathrm{1}+{i}}\right)^{{n}} {is}\:{a}\:+{ve}\:{integer}\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18
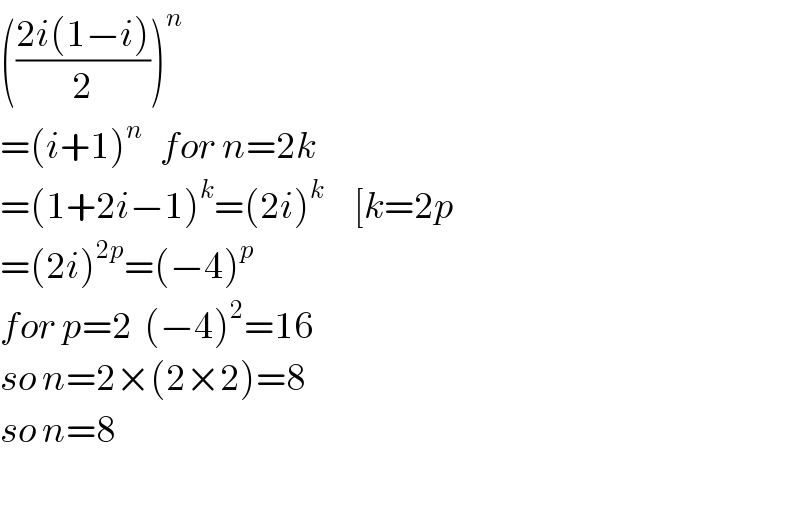
$$\left(\frac{\mathrm{2}{i}\left(\mathrm{1}−{i}\right)}{\mathrm{2}}\right)^{{n}} \\ $$$$=\left({i}+\mathrm{1}\right)^{{n}} \:\:\:{for}\:{n}=\mathrm{2}{k} \\ $$$$=\left(\mathrm{1}+\mathrm{2}{i}−\mathrm{1}\right)^{{k}} =\left(\mathrm{2}{i}\right)^{{k}} \:\:\:\:\:\left[{k}=\mathrm{2}{p}\right. \\ $$$$=\left(\mathrm{2}{i}\right)^{\mathrm{2}{p}} =\left(−\mathrm{4}\right)^{{p}} \\ $$$${for}\:{p}=\mathrm{2}\:\:\left(−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{16} \\ $$$${so}\:{n}=\mathrm{2}×\left(\mathrm{2}×\mathrm{2}\right)=\mathrm{8} \\ $$$${so}\:{n}=\mathrm{8}\: \\ $$$$ \\ $$
Commented by rahul 19 last updated on 04/Dec/18
thanks sir ����
