
Question Number 154036 by liberty last updated on 13/Sep/21
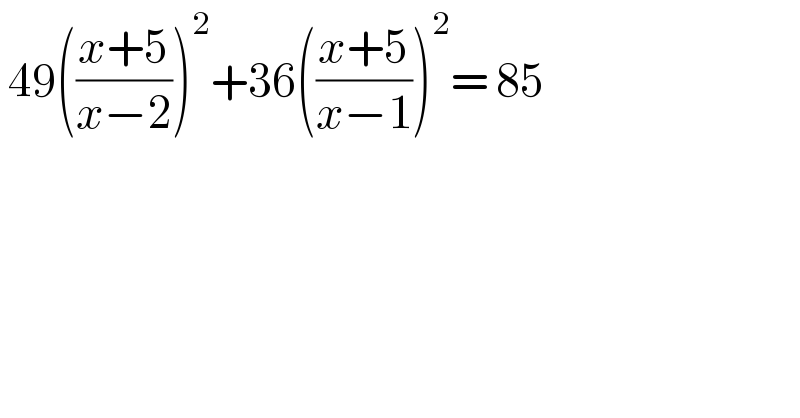
$$\:\mathrm{49}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{36}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{85} \\ $$
Answered by Rasheed.Sindhi last updated on 13/Sep/21
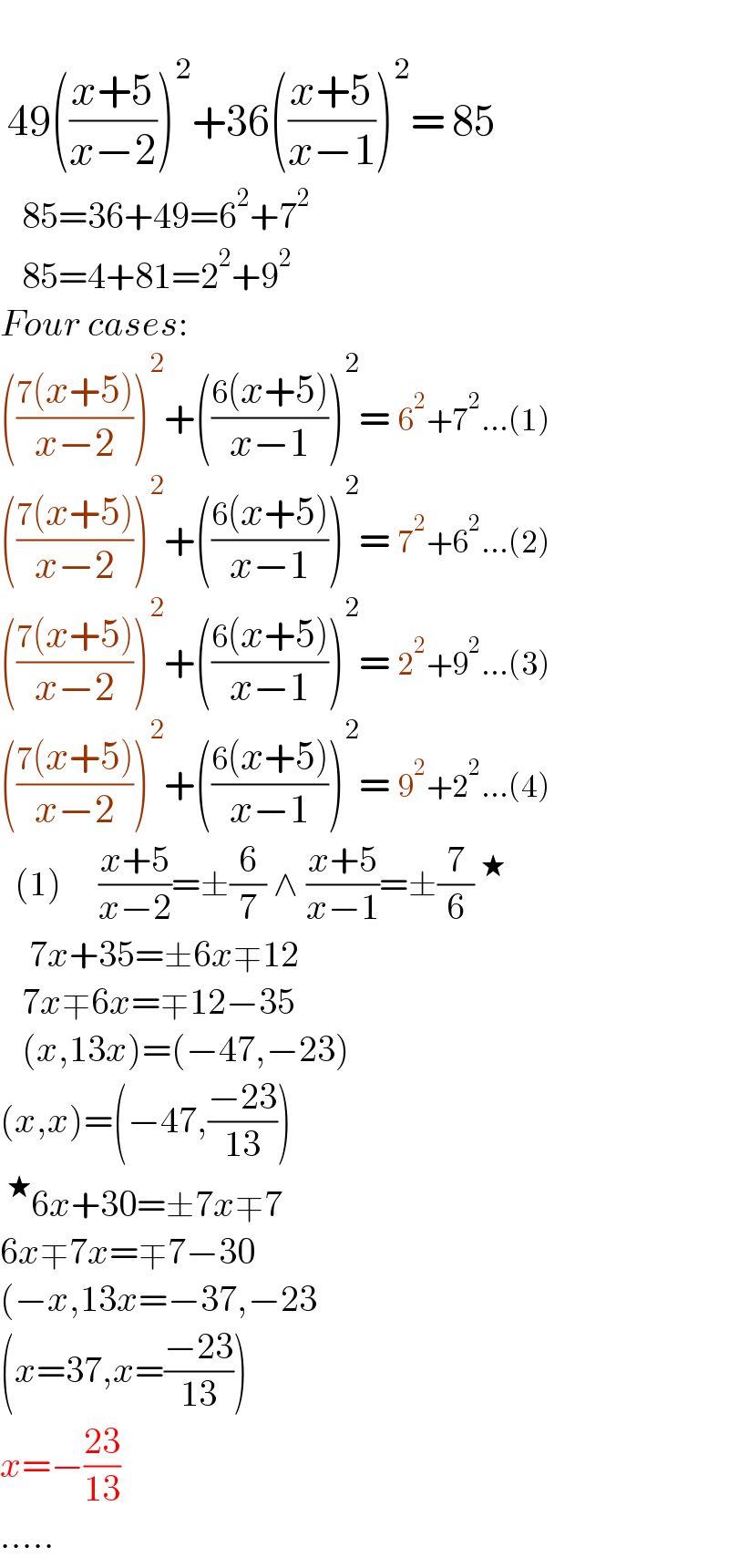
$$ \\ $$$$\:\mathrm{49}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{36}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{85} \\ $$$$\:\:\:\mathrm{85}=\mathrm{36}+\mathrm{49}=\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} \\ $$$$\:\:\:\mathrm{85}=\mathrm{4}+\mathrm{81}=\mathrm{2}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} \\ $$$${Four}\:{cases}: \\ $$$$\left(\frac{\mathrm{7}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{6}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} ...\left(\mathrm{1}\right) \\ $$$$\left(\frac{\mathrm{7}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{6}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{7}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} ...\left(\mathrm{2}\right) \\ $$$$\left(\frac{\mathrm{7}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{6}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{2}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} ...\left(\mathrm{3}\right) \\ $$$$\left(\frac{\mathrm{7}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{6}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{9}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} ...\left(\mathrm{4}\right) \\ $$$$\:\:\left(\mathrm{1}\right)\:\:\:\:\:\frac{{x}+\mathrm{5}}{{x}−\mathrm{2}}=\pm\frac{\mathrm{6}}{\mathrm{7}}\:\wedge\:\frac{{x}+\mathrm{5}}{{x}−\mathrm{1}}=\pm\frac{\mathrm{7}}{\mathrm{6}}\:^{\bigstar} \\ $$$$\:\:\:\:\mathrm{7}{x}+\mathrm{35}=\pm\mathrm{6}{x}\mp\mathrm{12} \\ $$$$\:\:\:\mathrm{7}{x}\mp\mathrm{6}{x}=\mp\mathrm{12}−\mathrm{35} \\ $$$$\:\:\:\left({x},\mathrm{13}{x}\right)=\left(−\mathrm{47},−\mathrm{23}\right) \\ $$$$\left({x},{x}\right)=\left(−\mathrm{47},\frac{−\mathrm{23}}{\mathrm{13}}\right) \\ $$$$\:^{\bigstar} \mathrm{6}{x}+\mathrm{30}=\pm\mathrm{7}{x}\mp\mathrm{7} \\ $$$$\mathrm{6}{x}\mp\mathrm{7}{x}=\mp\mathrm{7}−\mathrm{30} \\ $$$$\left(−{x},\mathrm{13}{x}=−\mathrm{37},−\mathrm{23}\right. \\ $$$$\left({x}=\mathrm{37},{x}=\frac{−\mathrm{23}}{\mathrm{13}}\right) \\ $$$${x}=−\frac{\mathrm{23}}{\mathrm{13}} \\ $$$$..... \\ $$
Commented by iloveisrael last updated on 14/Sep/21
$${waw}....{amazing} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Sep/21

$$\mathcal{T}{h}\alpha{n}\mathcal{X}\:\:{sir}! \\ $$
Answered by Rasheed.Sindhi last updated on 13/Sep/21

$$\:\underset{\mathrm{u}^{\mathrm{2}} } {\underbrace{\left(\frac{\mathrm{7}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{2}}\right)^{\mathrm{2}} }}+\underset{\mathrm{v}^{\mathrm{2}} } {\underbrace{\left(\frac{\mathrm{6}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{1}}\right)^{\mathrm{2}} }}=\:\mathrm{85} \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} =\mathrm{85} \\ $$$$\frac{\mathrm{7}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{2}}=\mathrm{u} \\ $$$$\mathrm{7}{x}+\mathrm{35}={ux}−\mathrm{2}{u}\Rightarrow{ux}−\mathrm{7}{x}=\mathrm{2}{u}+\mathrm{35} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}{u}+\mathrm{35}}{{u}−\mathrm{7}} \\ $$$$\mathrm{v}=\frac{\mathrm{6}\left({x}+\mathrm{5}\right)}{{x}−\mathrm{1}}\Rightarrow\mathrm{6}{x}+\mathrm{30}=\mathrm{v}{x}−\mathrm{v} \\ $$$${x}\left(\mathrm{v}−\mathrm{6}\right)=\mathrm{v}+\mathrm{30} \\ $$$$\left(\frac{\mathrm{2}{u}+\mathrm{35}}{{u}−\mathrm{7}}\right)\left(\mathrm{v}−\mathrm{6}\right)=\mathrm{v}+\mathrm{30} \\ $$$$\mathrm{v}\left(\frac{\mathrm{2}{u}+\mathrm{35}}{{u}−\mathrm{7}}\right)−\mathrm{6}\left(\frac{\mathrm{2}{u}+\mathrm{35}}{{u}−\mathrm{7}}\right)=\mathrm{v}+\mathrm{30} \\ $$$$\mathrm{v}\left(\frac{\mathrm{2}{u}+\mathrm{35}}{{u}−\mathrm{7}}\right)−\mathrm{v}=\mathrm{6}\left(\frac{\mathrm{2}{u}+\mathrm{35}}{{u}−\mathrm{7}}\right)+\mathrm{30} \\ $$$$\mathrm{v}\left(\frac{\mathrm{2}{u}+\mathrm{35}}{{u}−\mathrm{7}}−\mathrm{1}\right)=\frac{\mathrm{12u}+\cancel{\mathrm{210}}+\mathrm{30u}−\cancel{\mathrm{210}}}{\mathrm{u}−\mathrm{7}} \\ $$$$\mathrm{v}\left(\frac{\mathrm{2}{u}+\mathrm{35}−\mathrm{u}+\mathrm{7}}{{u}−\mathrm{7}}\right)=\frac{\mathrm{12u}+\mathrm{210}+\mathrm{30u}−\mathrm{210}}{\mathrm{u}−\mathrm{7}} \\ $$$$\mathrm{v}\left(\frac{{u}+\mathrm{42}}{{u}−\mathrm{7}}\right)=\frac{\mathrm{42u}}{\mathrm{u}−\mathrm{7}} \\ $$$$\mathrm{v}=\frac{\mathrm{42u}}{\mathrm{u}+\mathrm{42}} \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} =\mathrm{85}\Rightarrow\mathrm{u}^{\mathrm{2}} +\left(\frac{\mathrm{42u}}{\mathrm{u}+\mathrm{42}}\right)^{\mathrm{2}} =\mathrm{85} \\ $$$$\mathrm{u}^{\mathrm{2}} \left(\mathrm{u}+\mathrm{42}\right)^{\mathrm{2}} +\mathrm{42}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} −\mathrm{85}\left(\mathrm{u}+\mathrm{42}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{u}^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} +\mathrm{84u}+\mathrm{42}^{\mathrm{2}} \right)+\mathrm{42}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} −\mathrm{85}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{84u}+\mathrm{42}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{u}^{\mathrm{4}} +\mathrm{84u}^{\mathrm{3}} +\mathrm{42}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} +\mathrm{42}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} −\mathrm{85u}^{\mathrm{2}} −\mathrm{7140u}−\mathrm{85}\left(\mathrm{42}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{u}^{\mathrm{4}} +\mathrm{84u}^{\mathrm{3}} +\left(\mathrm{2}.\mathrm{42}^{\mathrm{2}} −\mathrm{85}\right)\mathrm{u}^{\mathrm{2}} −\mathrm{7140u}−\mathrm{85}\left(\mathrm{42}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$... \\ $$$$...... \\ $$$$.... \\ $$
Answered by MJS_new last updated on 13/Sep/21
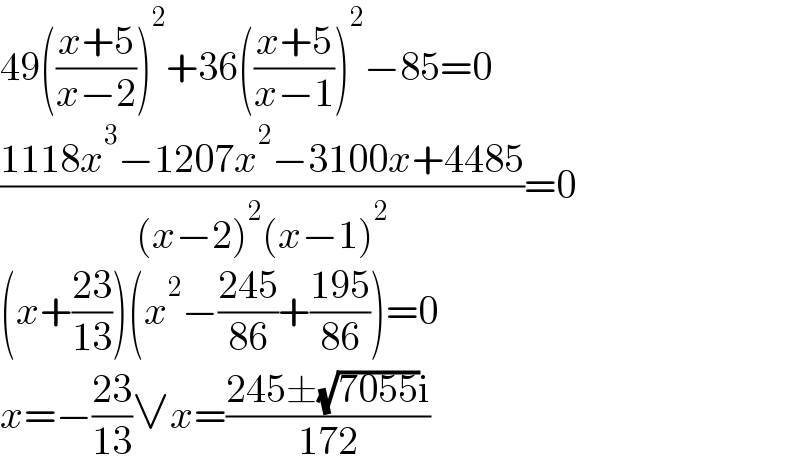
$$\mathrm{49}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{36}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{85}=\mathrm{0} \\ $$$$\frac{\mathrm{1118}{x}^{\mathrm{3}} −\mathrm{1207}{x}^{\mathrm{2}} −\mathrm{3100}{x}+\mathrm{4485}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{23}}{\mathrm{13}}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{245}}{\mathrm{86}}+\frac{\mathrm{195}}{\mathrm{86}}\right)=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{23}}{\mathrm{13}}\vee{x}=\frac{\mathrm{245}\pm\sqrt{\mathrm{7055}}\mathrm{i}}{\mathrm{172}} \\ $$
