
Question Number 48921 by peter frank last updated on 30/Nov/18

Commented by maxmathsup by imad last updated on 30/Nov/18
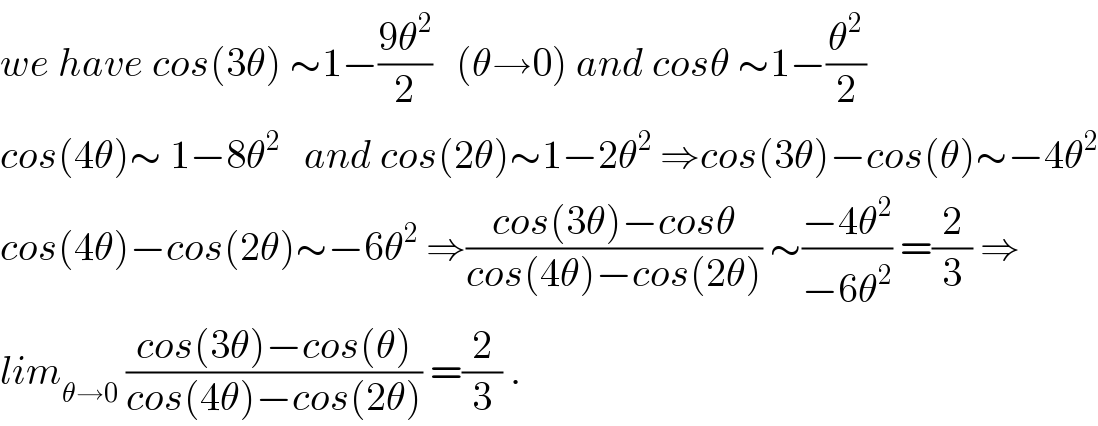
$${we}\:{have}\:{cos}\left(\mathrm{3}\theta\right)\:\sim\mathrm{1}−\frac{\mathrm{9}\theta^{\mathrm{2}} }{\mathrm{2}}\:\:\:\left(\theta\rightarrow\mathrm{0}\right)\:{and}\:{cos}\theta\:\sim\mathrm{1}−\frac{\theta^{\mathrm{2}} }{\mathrm{2}} \\ $$$${cos}\left(\mathrm{4}\theta\right)\sim\:\mathrm{1}−\mathrm{8}\theta^{\mathrm{2}} \:\:\:{and}\:{cos}\left(\mathrm{2}\theta\right)\sim\mathrm{1}−\mathrm{2}\theta^{\mathrm{2}} \:\Rightarrow{cos}\left(\mathrm{3}\theta\right)−{cos}\left(\theta\right)\sim−\mathrm{4}\theta^{\mathrm{2}} \\ $$$${cos}\left(\mathrm{4}\theta\right)−{cos}\left(\mathrm{2}\theta\right)\sim−\mathrm{6}\theta^{\mathrm{2}} \:\Rightarrow\frac{{cos}\left(\mathrm{3}\theta\right)−{cos}\theta}{{cos}\left(\mathrm{4}\theta\right)−{cos}\left(\mathrm{2}\theta\right)}\:\sim\frac{−\mathrm{4}\theta^{\mathrm{2}} }{−\mathrm{6}\theta^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$${lim}_{\theta\rightarrow\mathrm{0}} \:\frac{{cos}\left(\mathrm{3}\theta\right)−{cos}\left(\theta\right)}{{cos}\left(\mathrm{4}\theta\right)−{cos}\left(\mathrm{2}\theta\right)}\:=\frac{\mathrm{2}}{\mathrm{3}}\:. \\ $$
Answered by afachri last updated on 30/Nov/18

$$\Leftrightarrow\:\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\left(−\mathrm{2}\:{sin}\:\frac{\mathrm{3}\theta+\theta}{\mathrm{2}}{sin}\frac{\mathrm{3}\theta−\theta}{\mathrm{2}}\right)}{\left(−\mathrm{2}{sin}\frac{\mathrm{4}\theta+\mathrm{2}\theta}{\mathrm{2}}{sin}\frac{\mathrm{4}\theta−\mathrm{2}\theta}{\mathrm{2}}\right)}\:\: \\ $$$$ \\ $$$$\Leftrightarrow\:\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left(\frac{{sin}\mathrm{2}\theta{sin}\theta}{{sin}\mathrm{3}\theta{sin}\theta}\right) \\ $$$$ \\ $$$$\Leftrightarrow\:\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{sin}\mathrm{2}\theta}{\mathrm{sin3}\theta}\:.\:\frac{\mathrm{2}\theta}{\mathrm{2}\theta}\:.\:\frac{\mathrm{3}\theta}{\mathrm{3}\theta}\:\:=\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{sin}\mathrm{2}\theta}{\mathrm{2}\theta}\:.\:\frac{\mathrm{3}\theta}{{sin}\mathrm{3}\theta}\:.\:\frac{\mathrm{2}\theta}{\mathrm{3}\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{notice}}\::\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{ax}}}{\boldsymbol{{sin}}\left(\boldsymbol{{ax}}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{sin}}\left(\boldsymbol{{ax}}\right)}{\boldsymbol{{ax}}}\:=\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by peter frank last updated on 30/Nov/18

$$\mathrm{thank}\:\mathrm{you} \\ $$$$ \\ $$
Commented by afachri last updated on 30/Nov/18
$$\mathrm{your}\:\mathrm{welcome},\:\mathrm{Sir}. \\ $$
Answered by MJS last updated on 30/Nov/18

$$\left(\mathrm{2}\right) \\ $$$$\mathrm{put}\:\theta=\mathrm{2arctan}\:{t} \\ $$$${x}=−\frac{{a}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}{t}} \\ $$$${y}=−\frac{{a}\left({t}+\mathrm{1}\right)}{{t}−\mathrm{1}}\:\Rightarrow\:{t}=\frac{{y}−{a}}{{y}+{a}} \\ $$$${x}=−\frac{\mathrm{2}{a}^{\mathrm{3}} }{\left({y}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}\:\Leftrightarrow\:{y}=\pm{a}\sqrt{\frac{{x}−\mathrm{2}{a}}{{x}}} \\ $$
Answered by MJS last updated on 30/Nov/18

$$\left(\mathrm{2}\right) \\ $$$${x}=−\frac{{a}\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}{\mathrm{sin}\:\theta}\:\Rightarrow\:\mathrm{sin}\:\theta\:=\frac{{a}}{{a}−{x}} \\ $$$${y}=\frac{{a}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)}{\mathrm{cos}\:\theta}\:\Rightarrow\:\mathrm{cos}\:\theta\:=\frac{{a}\left({x}−\mathrm{2}{a}\right)}{\left({x}−{a}\right){y}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta\:+\mathrm{cos}^{\mathrm{2}} \:\theta\:=\mathrm{1} \\ $$$$\frac{{a}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{a}\left({x}−{a}\right)\right)}{{y}^{\mathrm{2}} \left({x}−{a}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\:{y}=\pm{a}\sqrt{\frac{{x}−\mathrm{2}{a}}{{x}}} \\ $$
