
Question Number 48869 by behi83417@gmail.com last updated on 29/Nov/18
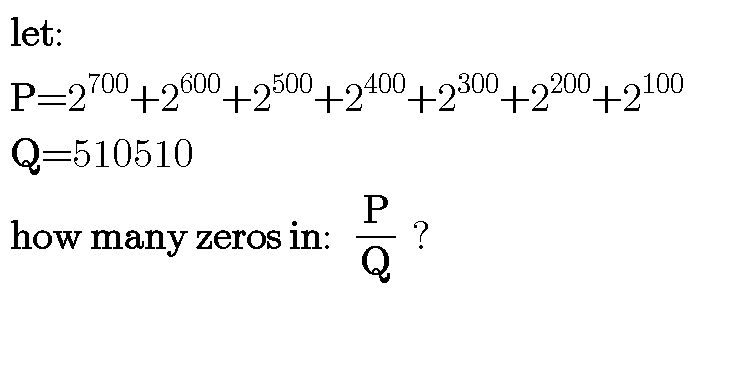
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18

$${i}\:{can}\:{not}\:{understand}\:{the}\:{questions}.. \\ $$$${let}\:\frac{{P}}{{Q}}={Intregal}\:{part}+{fractional}\:{part} \\ $$$${in}\:{which}\:{location}\:{zeros}\:{to}\:{find}.. \\ $$$$ \\ $$$$ \\ $$$$\:{s} \\ $$
Commented by behi83417@gmail.com last updated on 29/Nov/18
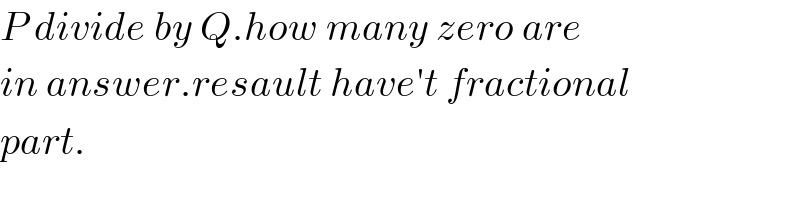
$${P}\:{divide}\:{by}\:{Q}.{how}\:{many}\:{zero}\:{are} \\ $$$${in}\:{answer}.{resault}\:{have}'{t}\:{fractional} \\ $$$${part}. \\ $$
Commented by Kunal12588 last updated on 30/Nov/18
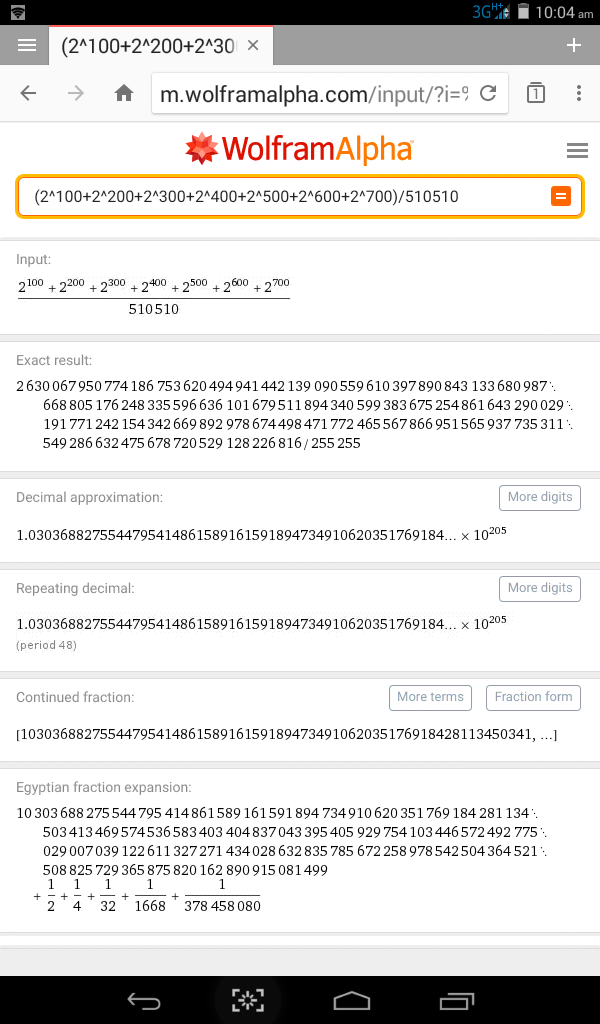
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Nov/18

$$\mathrm{2}^{\mathrm{1}} =\mathrm{2} \\ $$$$\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{3}} =\mathrm{8} \\ $$$$\mathrm{2}^{\mathrm{4}} =\mathrm{16} \\ $$$${so}\:{last}\:{digit}\:{of}\:\mathrm{2}^{\mathrm{4}} =\mathrm{6} \\ $$$${last}\:{digit}\:{of}\:\mathrm{2}^{\mathrm{100}} =\mathrm{6} \\ $$$${last}\:{digit}\:{of}\:{P}=\mathrm{2}\:\:\left(\mathrm{6}×\mathrm{7}=\mathrm{42}\right) \\ $$$${Q}=\mathrm{510510} \\ $$$$\:\:\:=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{13}×\mathrm{17} \\ $$$${let}\frac{{P}}{{Q}}={D}×\mathrm{10}^{{n}} \\ $$$${last}\:{digit}\:{of}\:{P}\:{is}\:\mathrm{2}\: \\ $$$${and}\:{Q}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{13}×\mathrm{17} \\ $$$${so}\:\:{P}\:{is}\:{devisible}\:{by}\:\mathrm{2}\:{contained}\:{in}\:\:{Q}\: \\ $$$${after}\:{division}\:{by}\:{two}\:{last}\:{digit}\:{of}\:{P}\:{is}\:\mathrm{1} \\ $$$${so}\:{again}\:{by}\:{division}\:\mathrm{3}×\mathrm{5}×\mathrm{7}×\mathrm{11}×\mathrm{13}×\mathrm{17} \\ $$$${last}\:{digit}\:{is}\:{either}\:\mathrm{3}\:{or}\:\mathrm{7} \\ $$$${so}\:{there}\:{will}\:{be}\:{no}\:{zeroes}\:{in}\:\frac{{P}}{{Q}}\: \\ $$$$ \\ $$$${pls}\:{check}\:{is}\:{it}\:{correct} \\ $$
