
Question Number 48851 by vajpaithegrate@gmail.com last updated on 29/Nov/18
![the total no of solution of sin{x}=cos{x} where{x} denotes fractional part of x in [o 2π]is equal to ans:6](Q48851.png)
$$\mathrm{the}\:\mathrm{total}\:\mathrm{no}\:\mathrm{of}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{sin}\left\{\mathrm{x}\right\}=\mathrm{cos}\left\{\mathrm{x}\right\} \\ $$$$\mathrm{where}\left\{\mathrm{x}\right\}\:\mathrm{denotes}\:\mathrm{fractional}\:\mathrm{part}\:\mathrm{of}\:\mathrm{x}\:\mathrm{in} \\ $$$$\left[\mathrm{o}\:\mathrm{2}\pi\right]\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{ans}:\mathrm{6} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18
![sin{x}=cos{x} sin(x−[x])=cos(x−[x]) x={x}+[x] {x}=fractional part function [x]=greatest integer function from graph it is seen that in [0,2π] six(06) solution](Q48856.png)
$${sin}\left\{{x}\right\}={cos}\left\{{x}\right\} \\ $$$${sin}\left({x}−\left[{x}\right]\right)={cos}\left({x}−\left[{x}\right]\right) \\ $$$${x}=\left\{{x}\right\}+\left[{x}\right] \\ $$$$\left\{{x}\right\}={fractional}\:{part}\:{function} \\ $$$$\left[{x}\right]={greatest}\:{integer}\:{function} \\ $$$${from}\:{graph}\:\:{it}\:{is}\:{seen}\:{that}\:{in}\:\left[\mathrm{0},\mathrm{2}\pi\right] \\ $$$${six}\left(\mathrm{06}\right)\:{solution} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18
![graph of sin{x} sin(x−[x]](Q48858.png)
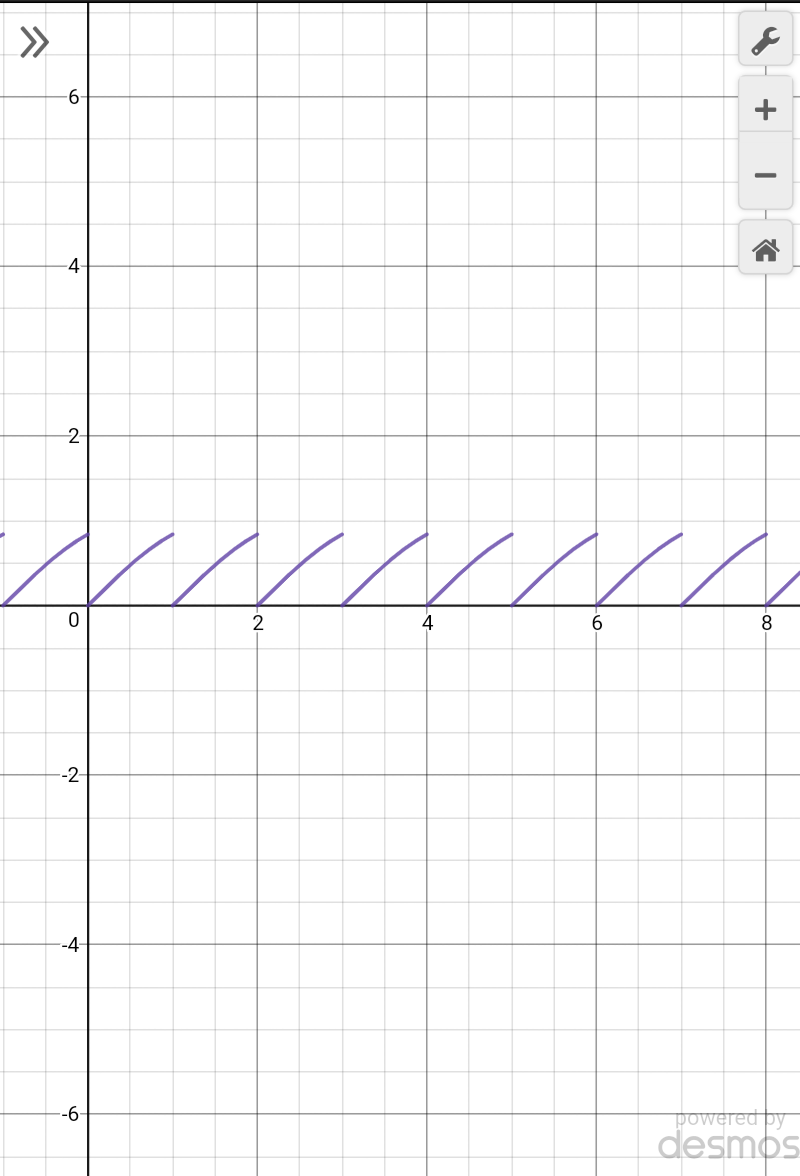
$${graph}\:{of}\:{sin}\left\{{x}\right\} \\ $$$${sin}\left({x}−\left[{x}\right]\right. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18
![graph of cos{x} graph of cos(x−[x])](Q48860.png)
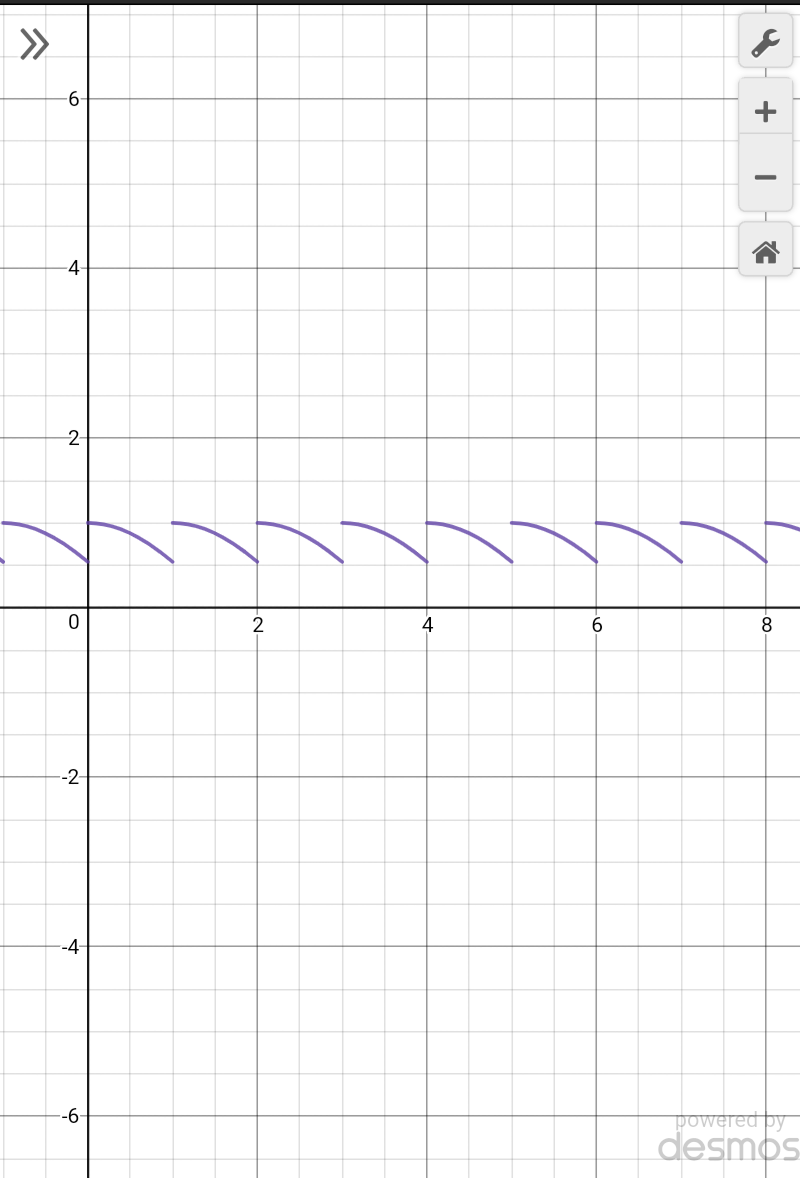
$${graph}\:{of}\:{cos}\left\{{x}\right\} \\ $$$${graph}\:{of}\:{cos}\left({x}−\left[{x}\right]\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18

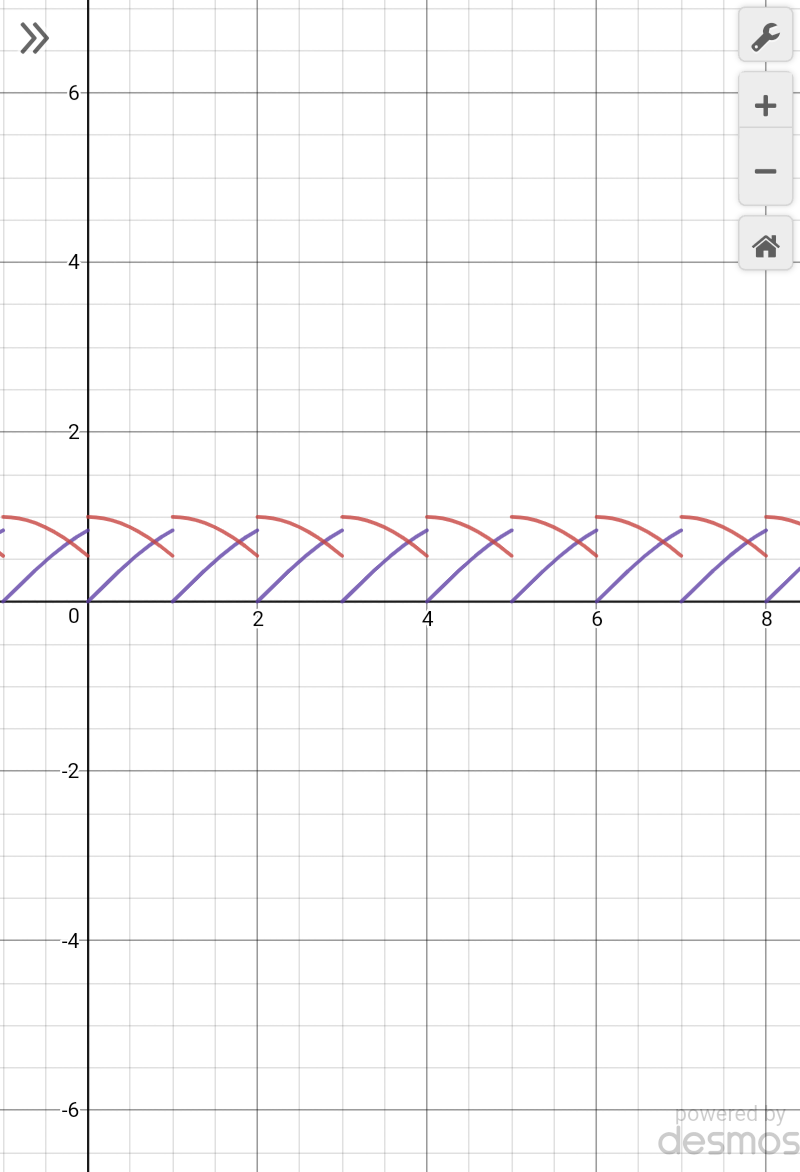
$$\mathrm{2}\pi=\mathrm{2}×\mathrm{3}.\mathrm{14}=\mathrm{6}.\mathrm{28} \\ $$$${in}\:{graph}\:\:{it}\:{is}\:{seen}\:{that}\:{from}\:{x}=\mathrm{0}\:{to}\:{x}=\mathrm{6} \\ $$$${there}\:{are}\:{six}\:{point}\:{where}\:{sin}\left\{{x}\right\}={cos}\left\{{x}\right\} \\ $$$${intersects}.\:\:{so}\:{six}\:{solution}\:{in}\:{x}\:\left(\mathrm{0},\mathrm{2}\pi\right) \\ $$
Commented by vajpaithegrate@gmail.com last updated on 29/Nov/18

$$\mathrm{tnq}\:\mathrm{sir} \\ $$
Commented by vajpaithegrate@gmail.com last updated on 29/Nov/18
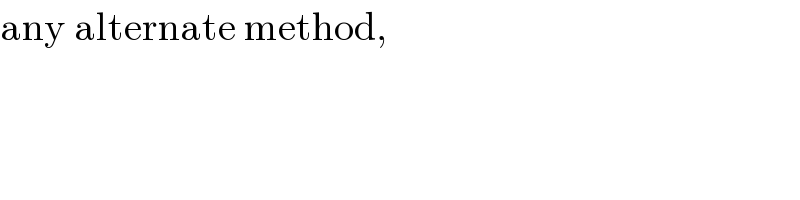
$$\mathrm{any}\:\mathrm{alternate}\:\mathrm{method}, \\ $$
Answered by mr W last updated on 29/Nov/18
![let t={x} 0≤t<1 sin t=cos t ⇒tan t=1 ⇒t=π/4=0.785 ⇒solution is x=n+t with n=0,1,2,.... i.e. x=0.785, 1.785, 2.785,...,5.785, 6.785,...... 2π=6.283<6.785 ⇒6 solutions within [0, 2π]: x=0.785, 1.785, 2.785,...,5.785](Q48864.png)
$${let}\:{t}=\left\{{x}\right\} \\ $$$$\mathrm{0}\leqslant{t}<\mathrm{1} \\ $$$$\mathrm{sin}\:{t}=\mathrm{cos}\:{t} \\ $$$$\Rightarrow\mathrm{tan}\:{t}=\mathrm{1} \\ $$$$\Rightarrow{t}=\pi/\mathrm{4}=\mathrm{0}.\mathrm{785} \\ $$$$\Rightarrow{solution}\:{is}\:{x}={n}+{t}\:{with}\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},.... \\ $$$${i}.{e}.\:{x}=\mathrm{0}.\mathrm{785},\:\mathrm{1}.\mathrm{785},\:\mathrm{2}.\mathrm{785},...,\mathrm{5}.\mathrm{785},\:\mathrm{6}.\mathrm{785},...... \\ $$$$\mathrm{2}\pi=\mathrm{6}.\mathrm{283}<\mathrm{6}.\mathrm{785} \\ $$$$\Rightarrow\mathrm{6}\:{solutions}\:{within}\:\left[\mathrm{0},\:\mathrm{2}\pi\right]: \\ $$$${x}=\mathrm{0}.\mathrm{785},\:\mathrm{1}.\mathrm{785},\:\mathrm{2}.\mathrm{785},...,\mathrm{5}.\mathrm{785} \\ $$
Commented by vajpaithegrate@gmail.com last updated on 29/Nov/18

$$\mathrm{tnq}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18

$${excellent}\:{sir}... \\ $$
