
Question Number 48763 by mr W last updated on 28/Nov/18
Commented by mr W last updated on 28/Nov/18
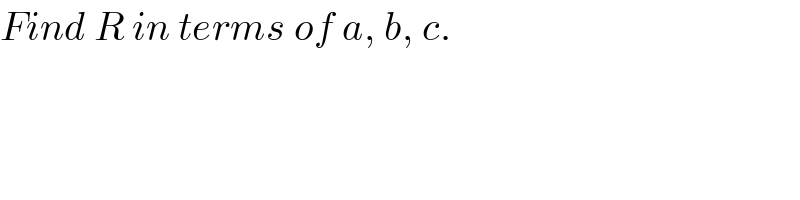
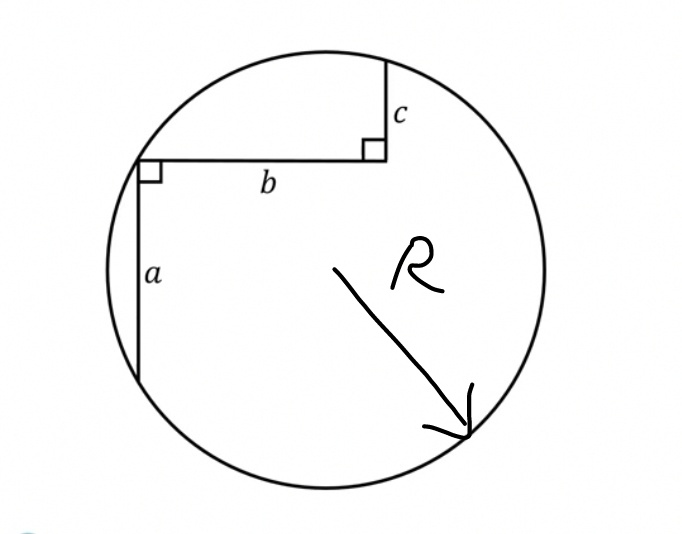
$${Find}\:{R}\:{in}\:{terms}\:{of}\:{a},\:{b},\:{c}. \\ $$
Answered by ajfour last updated on 28/Nov/18
Answered by ajfour last updated on 28/Nov/18
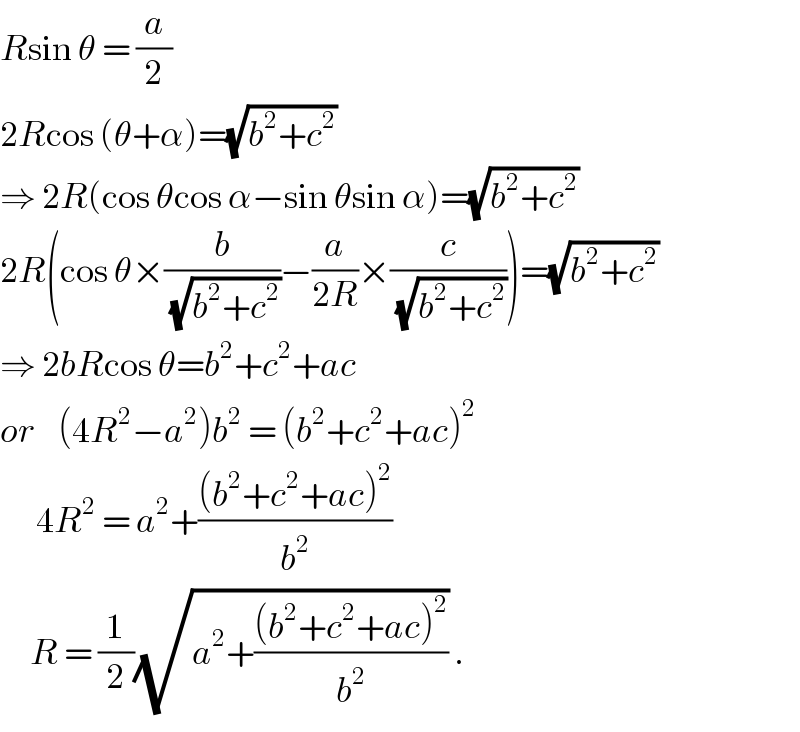
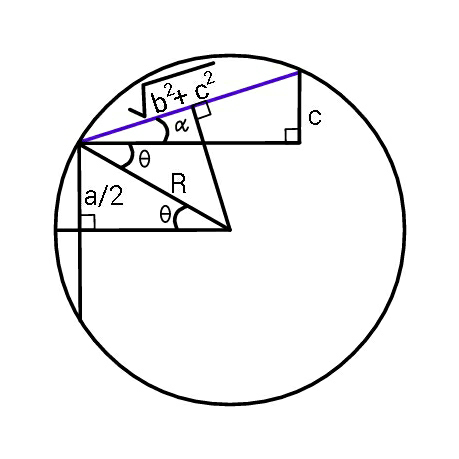
$${R}\mathrm{sin}\:\theta\:=\:\frac{{a}}{\mathrm{2}} \\ $$$$\mathrm{2}{R}\mathrm{cos}\:\left(\theta+\alpha\right)=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{2}{R}\left(\mathrm{cos}\:\theta\mathrm{cos}\:\alpha−\mathrm{sin}\:\theta\mathrm{sin}\:\alpha\right)=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\mathrm{2}{R}\left(\mathrm{cos}\:\theta×\frac{{b}}{\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}−\frac{{a}}{\mathrm{2}{R}}×\frac{{c}}{\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\right)=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{2}{bR}\mathrm{cos}\:\theta={b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ac} \\ $$$${or}\:\:\:\:\left(\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){b}^{\mathrm{2}} \:=\:\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ac}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{4}{R}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} +\frac{\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ac}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:{R}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} +\frac{\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ac}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }}\:. \\ $$
Commented by mr W last updated on 28/Nov/18
$${correct}!\:{thank}\:{you}\:{sir}! \\ $$
Commented by mr W last updated on 28/Nov/18

$${alternative}\:{way}: \\ $$$${circumcircle}\:{of}\:{a}\:{triangle}\:{with}\:{sides}: \\ $$$${a} \\ $$$$\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\sqrt{{b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${R}=\frac{{a}\sqrt{\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} \right)}}{\mathrm{4}{A}} \\ $$$${A}=\frac{{ab}}{\mathrm{2}} \\ $$$${R}=\frac{{a}\sqrt{\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} \right)}}{\mathrm{2}{ab}} \\ $$$$\Rightarrow{R}=\frac{\sqrt{\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} \right)}}{\mathrm{2}{b}} \\ $$
