
Question Number 48735 by Pk1167156@gmail.com last updated on 28/Nov/18
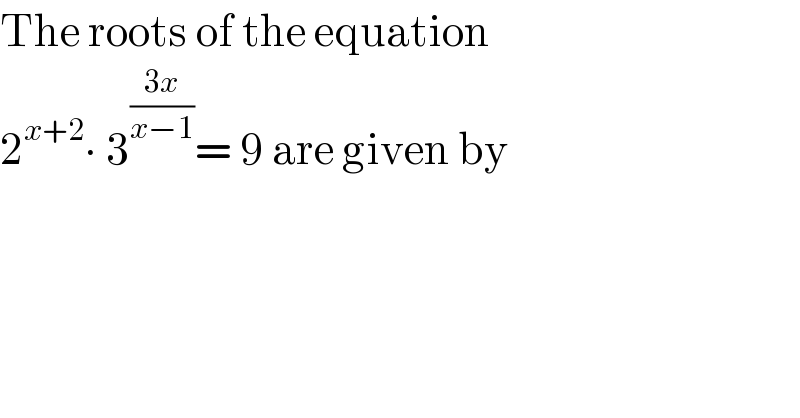
$$\mathrm{The}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\mathrm{2}^{{x}+\mathrm{2}} \centerdot\:\mathrm{3}^{\frac{\mathrm{3}{x}}{{x}−\mathrm{1}}} =\:\mathrm{9}\:\mathrm{are}\:\mathrm{given}\:\mathrm{by} \\ $$
Answered by Smail last updated on 28/Nov/18
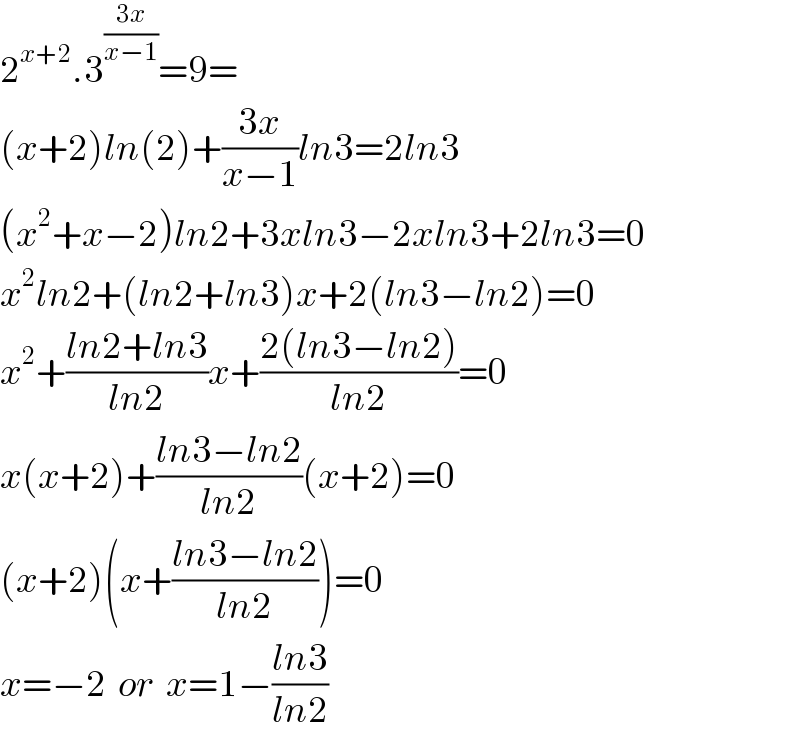
$$\mathrm{2}^{{x}+\mathrm{2}} .\mathrm{3}^{\frac{\mathrm{3}{x}}{{x}−\mathrm{1}}} =\mathrm{9}= \\ $$$$\left({x}+\mathrm{2}\right){ln}\left(\mathrm{2}\right)+\frac{\mathrm{3}{x}}{{x}−\mathrm{1}}{ln}\mathrm{3}=\mathrm{2}{ln}\mathrm{3} \\ $$$$\left({x}^{\mathrm{2}} +{x}−\mathrm{2}\right){ln}\mathrm{2}+\mathrm{3}{xln}\mathrm{3}−\mathrm{2}{xln}\mathrm{3}+\mathrm{2}{ln}\mathrm{3}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} {ln}\mathrm{2}+\left({ln}\mathrm{2}+{ln}\mathrm{3}\right){x}+\mathrm{2}\left({ln}\mathrm{3}−{ln}\mathrm{2}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\frac{{ln}\mathrm{2}+{ln}\mathrm{3}}{{ln}\mathrm{2}}{x}+\frac{\mathrm{2}\left({ln}\mathrm{3}−{ln}\mathrm{2}\right)}{{ln}\mathrm{2}}=\mathrm{0} \\ $$$${x}\left({x}+\mathrm{2}\right)+\frac{{ln}\mathrm{3}−{ln}\mathrm{2}}{{ln}\mathrm{2}}\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{2}\right)\left({x}+\frac{{ln}\mathrm{3}−{ln}\mathrm{2}}{{ln}\mathrm{2}}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{2}\:\:{or}\:\:{x}=\mathrm{1}−\frac{{ln}\mathrm{3}}{{ln}\mathrm{2}} \\ $$
