
Question Number 48560 by behi83417@gmail.com last updated on 25/Nov/18
Commented by behi83417@gmail.com last updated on 25/Nov/18
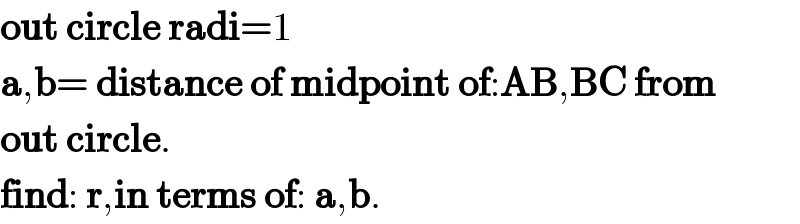
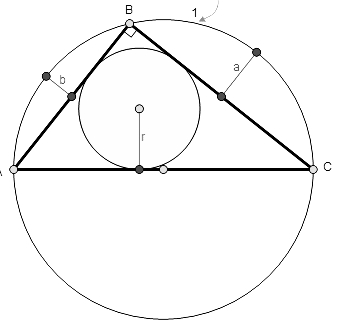
$$\boldsymbol{\mathrm{out}}\:\boldsymbol{\mathrm{circle}}\:\boldsymbol{\mathrm{radi}}=\mathrm{1} \\ $$$$\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}=\:\boldsymbol{\mathrm{distance}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{midpoint}}\:\boldsymbol{\mathrm{of}}:\boldsymbol{\mathrm{AB}},\boldsymbol{\mathrm{BC}}\:\boldsymbol{\mathrm{from}} \\ $$$$\boldsymbol{\mathrm{out}}\:\boldsymbol{\mathrm{circle}}. \\ $$$$\boldsymbol{\mathrm{find}}:\:\boldsymbol{\mathrm{r}},\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{terms}}\:\boldsymbol{\mathrm{of}}:\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}. \\ $$
Answered by mr W last updated on 25/Nov/18
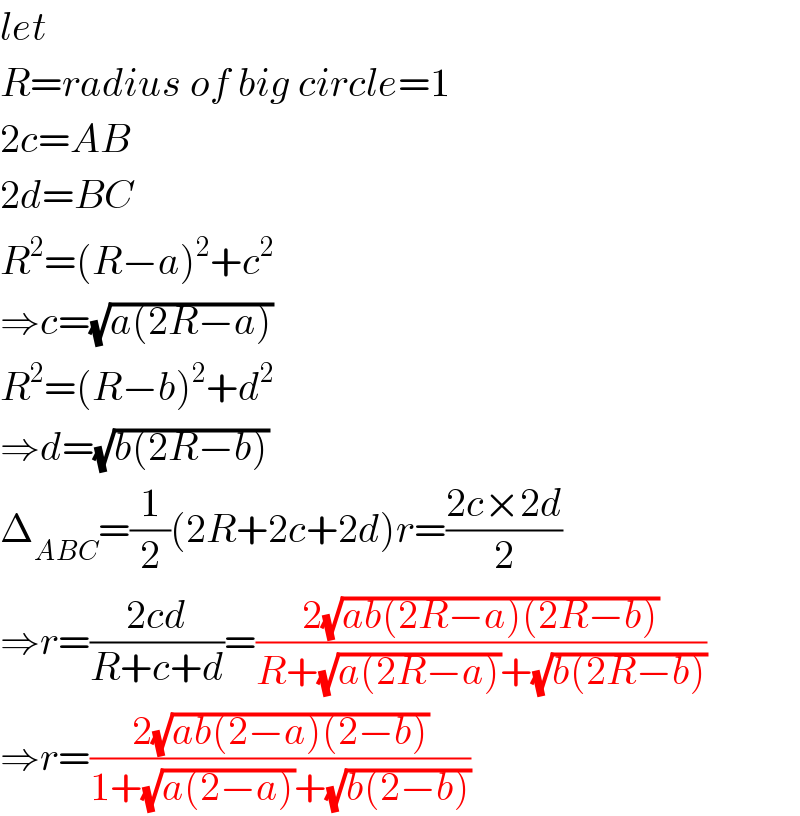
$${let} \\ $$$${R}={radius}\:{of}\:{big}\:{circle}=\mathrm{1} \\ $$$$\mathrm{2}{c}={AB} \\ $$$$\mathrm{2}{d}={BC} \\ $$$${R}^{\mathrm{2}} =\left({R}−{a}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\Rightarrow{c}=\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)} \\ $$$${R}^{\mathrm{2}} =\left({R}−{b}\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \\ $$$$\Rightarrow{d}=\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)} \\ $$$$\Delta_{{ABC}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{R}+\mathrm{2}{c}+\mathrm{2}{d}\right){r}=\frac{\mathrm{2}{c}×\mathrm{2}{d}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}{cd}}{{R}+{c}+{d}}=\frac{\mathrm{2}\sqrt{{ab}\left(\mathrm{2}{R}−{a}\right)\left(\mathrm{2}{R}−{b}\right)}}{{R}+\sqrt{{a}\left(\mathrm{2}{R}−{a}\right)}+\sqrt{{b}\left(\mathrm{2}{R}−{b}\right)}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}\sqrt{{ab}\left(\mathrm{2}−{a}\right)\left(\mathrm{2}−{b}\right)}}{\mathrm{1}+\sqrt{{a}\left(\mathrm{2}−{a}\right)}+\sqrt{{b}\left(\mathrm{2}−{b}\right)}} \\ $$
Commented by behi83417@gmail.com last updated on 25/Nov/18

$${dear}\:{master}!\:{i}\:{think}: \\ $$$$\mathrm{2}{c}={BC},\mathrm{2}{d}={AB},{you}\:{are}\:{say}.{am}\:{i}\:{right}? \\ $$$${ofcourse}\:{this}\:{is}\:{not}\:{important}\:{in}\:{final} \\ $$$${resault}. \\ $$
Commented by mr W last updated on 25/Nov/18
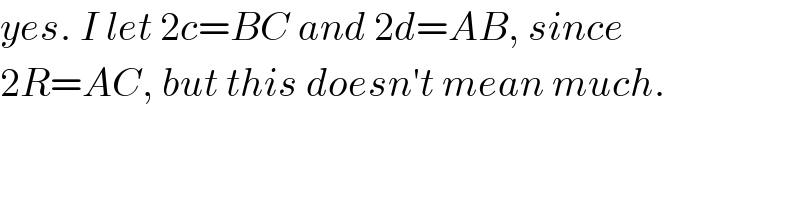
$${yes}.\:{I}\:{let}\:\mathrm{2}{c}={BC}\:{and}\:\mathrm{2}{d}={AB},\:{since} \\ $$$$\mathrm{2}{R}={AC},\:{but}\:{this}\:{doesn}'{t}\:{mean}\:{much}. \\ $$
