
Question Number 48529 by Pk1167156@gmail.com last updated on 25/Nov/18
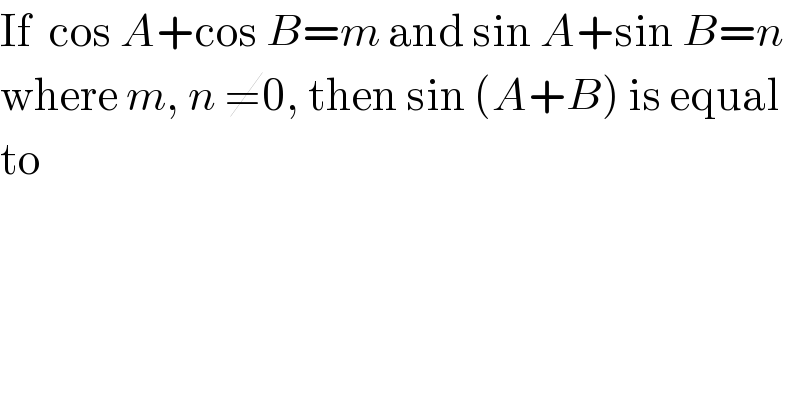
$$\mathrm{If}\:\:\mathrm{cos}\:{A}+\mathrm{cos}\:{B}={m}\:\mathrm{and}\:\mathrm{sin}\:{A}+\mathrm{sin}\:{B}={n} \\ $$$$\mathrm{where}\:{m},\:{n}\:\neq\mathrm{0},\:\mathrm{then}\:\mathrm{sin}\:\left({A}+{B}\right)\:\mathrm{is}\:\mathrm{equal} \\ $$$$\mathrm{to} \\ $$
Answered by math1967 last updated on 25/Nov/18

$$\frac{\mathrm{2}{mn}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }\: \\ $$
Answered by Kunal12588 last updated on 25/Nov/18
![cosA+cosB=m ⇒cos^2 A+cos^2 B+2cosAcosB=m^2 (1) sinA+sinB=n ⇒sin^2 A+sin^2 B+2sinAsinB=n^2 (2) add (1) and (2) ⇒1+1+2(cosAcosB+sinAsinB)=m^2 +n^2 ⇒2(1+cos(A−B))=m^2 +n^2 ⇒1+cos(A−B)=((m^2 +n^2 )/2) (3) (cosA+cosB)(sinA+sinB)=mn ⇒sinAcosA+sinAcosB+sinBcosA+sinAcosB=mn ⇒(1/2)sin2A+(1/2)sin2B+sin(A+B)=mn ⇒(1/2){2sin(A+B)cos(A−B)}+sin(A+B)=mn ⇒sin(A+B){1+cos(A−B)}=mn ⇒sin(A+B)(((m^2 +n^2 )/2))=mn [from (3)] ⇒sin(A+B)=((2mn)/(m^2 +n^2 ))](Q48542.png)
$${cosA}+{cosB}={m} \\ $$$$\Rightarrow{cos}^{\mathrm{2}} {A}+{cos}^{\mathrm{2}} {B}+\mathrm{2}{cosAcosB}={m}^{\mathrm{2}} \:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$${sinA}+{sinB}={n} \\ $$$$\Rightarrow{sin}^{\mathrm{2}} {A}+{sin}^{\mathrm{2}} {B}+\mathrm{2}{sinAsinB}={n}^{\mathrm{2}} \:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${add}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{1}+\mathrm{1}+\mathrm{2}\left({cosAcosB}+{sinAsinB}\right)={m}^{\mathrm{2}} +{n}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}+{cos}\left({A}−{B}\right)\right)={m}^{\mathrm{2}} +{n}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}+{cos}\left({A}−{B}\right)=\frac{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\left({cosA}+{cosB}\right)\left({sinA}+{sinB}\right)={mn} \\ $$$$\Rightarrow{sinAcosA}+{sinAcosB}+{sinBcosA}+{sinAcosB}={mn} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{A}+\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{B}+{sin}\left({A}+{B}\right)={mn} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}{sin}\left({A}+{B}\right){cos}\left({A}−{B}\right)\right\}+{sin}\left({A}+{B}\right)={mn} \\ $$$$\Rightarrow{sin}\left({A}+{B}\right)\left\{\mathrm{1}+{cos}\left({A}−{B}\right)\right\}={mn} \\ $$$$\Rightarrow{sin}\left({A}+{B}\right)\left(\frac{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }{\mathrm{2}}\right)={mn}\:\:\:\:\:\:\left[{from}\:\:\left(\mathrm{3}\right)\right] \\ $$$$\Rightarrow\boldsymbol{{sin}}\left(\boldsymbol{{A}}+\boldsymbol{{B}}\right)=\frac{\mathrm{2}\boldsymbol{{mn}}}{\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{n}}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Nov/18
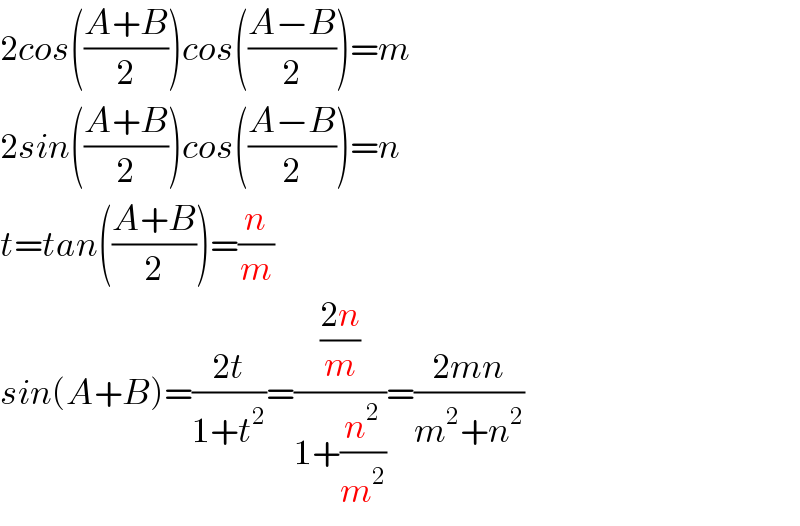
$$\mathrm{2}{cos}\left(\frac{{A}+{B}}{\mathrm{2}}\right){cos}\left(\frac{{A}−{B}}{\mathrm{2}}\right)={m} \\ $$$$\mathrm{2}{sin}\left(\frac{{A}+{B}}{\mathrm{2}}\right){cos}\left(\frac{{A}−{B}}{\mathrm{2}}\right)={n} \\ $$$${t}={tan}\left(\frac{{A}+{B}}{\mathrm{2}}\right)=\frac{{n}}{{m}}\: \\ $$$${sin}\left({A}+{B}\right)=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{\frac{\mathrm{2}{n}}{{m}}}{\mathrm{1}+\frac{{n}^{\mathrm{2}} }{{m}^{\mathrm{2}} }}=\frac{\mathrm{2}{mn}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$
Commented by Kunal12588 last updated on 26/Nov/18
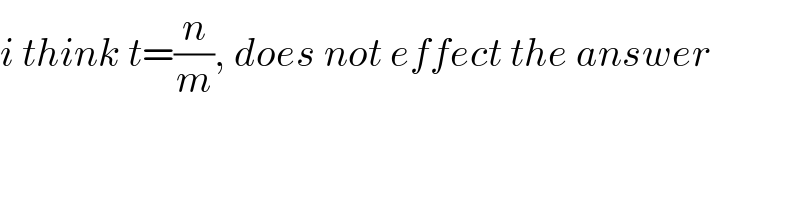
$${i}\:{think}\:{t}=\frac{{n}}{{m}},\:{does}\:{not}\:{effect}\:{the}\:{answer} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Nov/18
$${yes}\:\:{let}\:{me}\:{rectify}...{thank}\:{you}... \\ $$
