
Question Number 48447 by rahul 19 last updated on 24/Nov/18
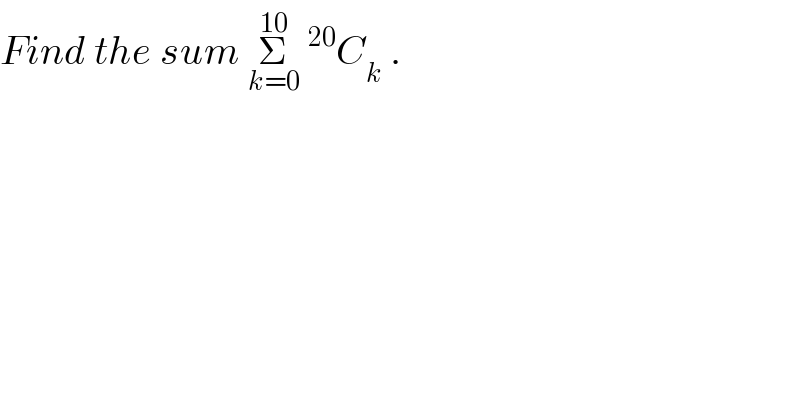
$${Find}\:{the}\:{sum}\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\:^{\mathrm{20}} {C}_{{k}} \:. \\ $$
Commented by rahul 19 last updated on 24/Nov/18

$${i}\:{think}\:\mathrm{2}^{{nd}} \:{last}\:{line}\:{is}\:{wrong}... \\ $$$$\mathrm{3}\:{times}\:^{\mathrm{20}} {C}_{\mathrm{10}} \:{has}\:{been}\:{taken}\:..... \\ $$$${plss}\:{also}\:{tell}\:{final}\:{correct}\:{answer}.... \\ $$
Commented by rahul 19 last updated on 24/Nov/18
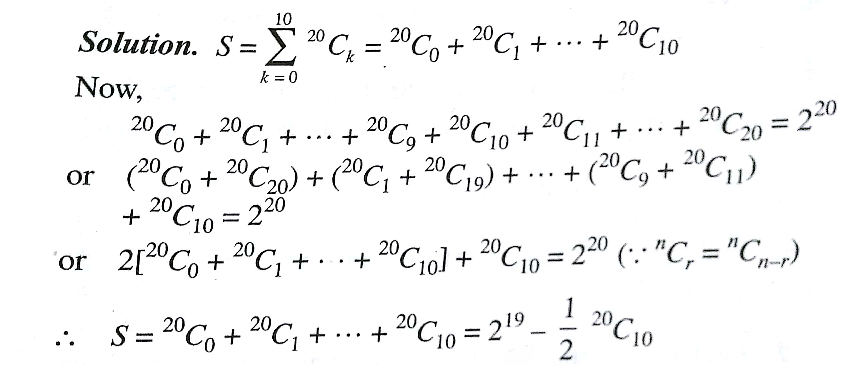
Commented by mr W last updated on 24/Nov/18
![S=C_0 ^(20) +C_1 ^(20) +C_2 ^(20) +C_3 ^(20) +...+C_(10) ^(20) C_0 ^(20) +C_1 ^(20) +C_2 ^(20) +C_3 ^(20) +...+C_(10) ^(20) +C_(11) ^(20) +...+C_(20) ^(20) =2^(20) [(C_0 ^(20) +C_(20) ^(20) )+(C_1 ^(20) +C_(19) ^(20) )+...+(C_(10) ^(20) +C_(10) ^(20) )]−C_(10) ^(20) =2^(20) [2C_0 ^(20) +2C_1 ^(20) +...+2C_(10) ^(20) ]−C_(10) ^(20) =2^(20) 2[C_0 ^(20) +C_1 ^(20) +...+C_(10) ^(20) ]−C_(10) ^(20) =2^(20) 2S−C_(10) ^(20) =2^(20) ⇒S=2^(19) +(C_(10) ^(20) /2)](Q48456.png)
$${S}={C}_{\mathrm{0}} ^{\mathrm{20}} +{C}_{\mathrm{1}} ^{\mathrm{20}} +{C}_{\mathrm{2}} ^{\mathrm{20}} +{C}_{\mathrm{3}} ^{\mathrm{20}} +...+{C}_{\mathrm{10}} ^{\mathrm{20}} \\ $$$${C}_{\mathrm{0}} ^{\mathrm{20}} +{C}_{\mathrm{1}} ^{\mathrm{20}} +{C}_{\mathrm{2}} ^{\mathrm{20}} +{C}_{\mathrm{3}} ^{\mathrm{20}} +...+{C}_{\mathrm{10}} ^{\mathrm{20}} +{C}_{\mathrm{11}} ^{\mathrm{20}} +...+{C}_{\mathrm{20}} ^{\mathrm{20}} =\mathrm{2}^{\mathrm{20}} \\ $$$$\left[\left({C}_{\mathrm{0}} ^{\mathrm{20}} +{C}_{\mathrm{20}} ^{\mathrm{20}} \right)+\left({C}_{\mathrm{1}} ^{\mathrm{20}} +{C}_{\mathrm{19}} ^{\mathrm{20}} \right)+...+\left({C}_{\mathrm{10}} ^{\mathrm{20}} +{C}_{\mathrm{10}} ^{\mathrm{20}} \right)\right]−{C}_{\mathrm{10}} ^{\mathrm{20}} =\mathrm{2}^{\mathrm{20}} \\ $$$$\left[\mathrm{2}{C}_{\mathrm{0}} ^{\mathrm{20}} +\mathrm{2}{C}_{\mathrm{1}} ^{\mathrm{20}} +...+\mathrm{2}{C}_{\mathrm{10}} ^{\mathrm{20}} \right]−{C}_{\mathrm{10}} ^{\mathrm{20}} =\mathrm{2}^{\mathrm{20}} \\ $$$$\mathrm{2}\left[{C}_{\mathrm{0}} ^{\mathrm{20}} +{C}_{\mathrm{1}} ^{\mathrm{20}} +...+{C}_{\mathrm{10}} ^{\mathrm{20}} \right]−{C}_{\mathrm{10}} ^{\mathrm{20}} =\mathrm{2}^{\mathrm{20}} \\ $$$$\mathrm{2}{S}−{C}_{\mathrm{10}} ^{\mathrm{20}} =\mathrm{2}^{\mathrm{20}} \\ $$$$\Rightarrow{S}=\mathrm{2}^{\mathrm{19}} +\frac{{C}_{\mathrm{10}} ^{\mathrm{20}} }{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 24/Nov/18
thanks sir ����
