
Question Number 4839 by FilupSmith last updated on 17/Mar/16
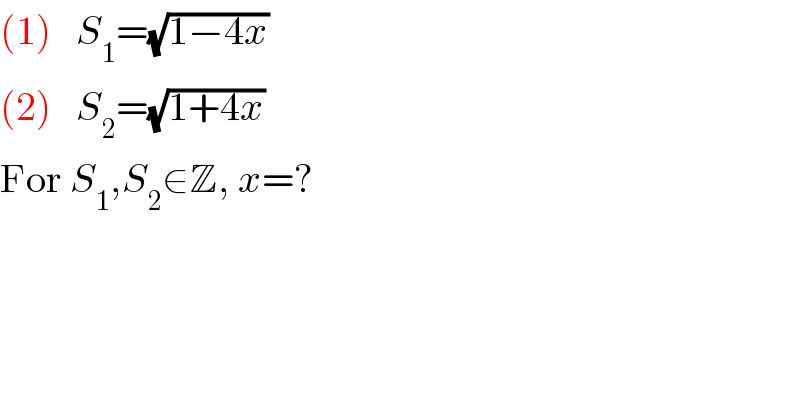
$$\left(\mathrm{1}\right)\:\:\:{S}_{\mathrm{1}} =\sqrt{\mathrm{1}−\mathrm{4}{x}} \\ $$$$\left(\mathrm{2}\right)\:\:\:{S}_{\mathrm{2}} =\sqrt{\mathrm{1}+\mathrm{4}{x}} \\ $$$$\mathrm{For}\:{S}_{\mathrm{1}} ,{S}_{\mathrm{2}} \in\mathbb{Z},\:{x}=? \\ $$
Commented by Yozzii last updated on 17/Mar/16
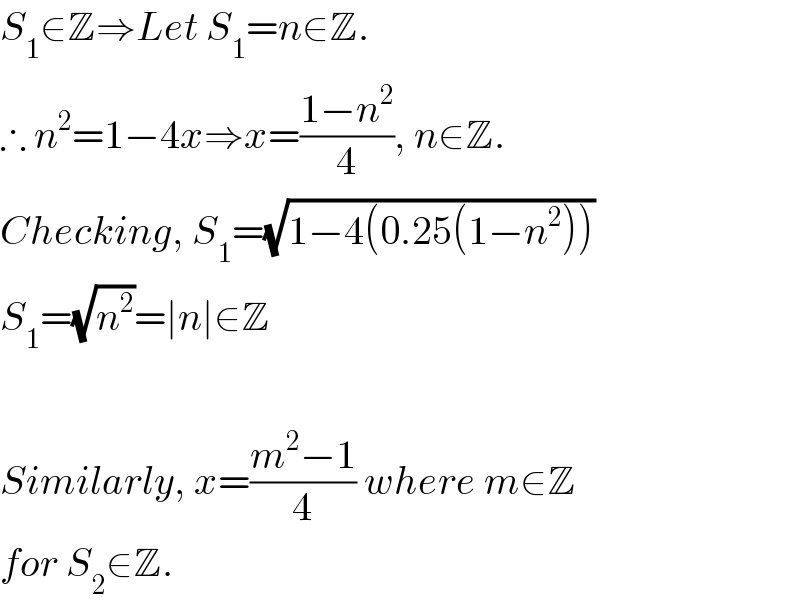
$${S}_{\mathrm{1}} \in\mathbb{Z}\Rightarrow{Let}\:{S}_{\mathrm{1}} ={n}\in\mathbb{Z}. \\ $$$$\therefore\:{n}^{\mathrm{2}} =\mathrm{1}−\mathrm{4}{x}\Rightarrow{x}=\frac{\mathrm{1}−{n}^{\mathrm{2}} }{\mathrm{4}},\:{n}\in\mathbb{Z}. \\ $$$${Checking},\:{S}_{\mathrm{1}} =\sqrt{\mathrm{1}−\mathrm{4}\left(\mathrm{0}.\mathrm{25}\left(\mathrm{1}−{n}^{\mathrm{2}} \right)\right)} \\ $$$${S}_{\mathrm{1}} =\sqrt{{n}^{\mathrm{2}} }=\mid{n}\mid\in\mathbb{Z} \\ $$$$ \\ $$$${Similarly},\:{x}=\frac{{m}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}\:{where}\:{m}\in\mathbb{Z}\: \\ $$$${for}\:{S}_{\mathrm{2}} \in\mathbb{Z}. \\ $$
Answered by Rasheed Soomro last updated on 17/Mar/16
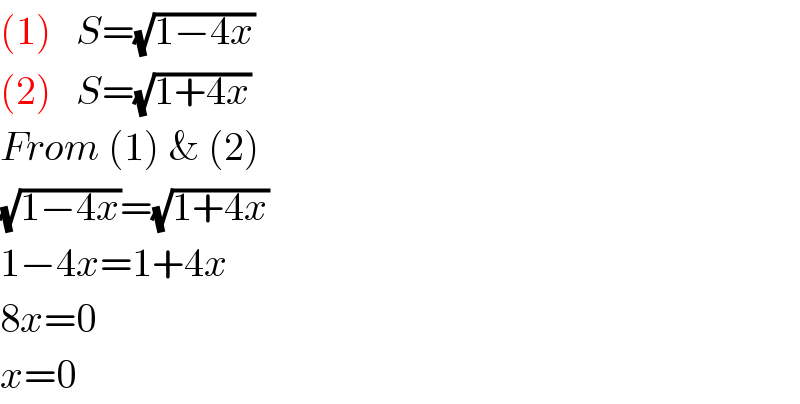
$$\left(\mathrm{1}\right)\:\:\:{S}=\sqrt{\mathrm{1}−\mathrm{4}{x}} \\ $$$$\left(\mathrm{2}\right)\:\:\:{S}=\sqrt{\mathrm{1}+\mathrm{4}{x}} \\ $$$${From}\:\left(\mathrm{1}\right)\:\&\:\left(\mathrm{2}\right) \\ $$$$\sqrt{\mathrm{1}−\mathrm{4}{x}}=\sqrt{\mathrm{1}+\mathrm{4}{x}} \\ $$$$\mathrm{1}−\mathrm{4}{x}=\mathrm{1}+\mathrm{4}{x} \\ $$$$\mathrm{8}{x}=\mathrm{0} \\ $$$${x}=\mathrm{0} \\ $$
Commented by FilupSmith last updated on 17/Mar/16

$$\mathrm{sorry},\:\mathrm{didn}'\mathrm{t}\:\mathrm{ask}\:\mathrm{properly}.\:\mathrm{I}\:\mathrm{meant}\:\mathrm{that} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{are}\:\mathrm{different}\:\mathrm{questions} \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 18/Mar/16
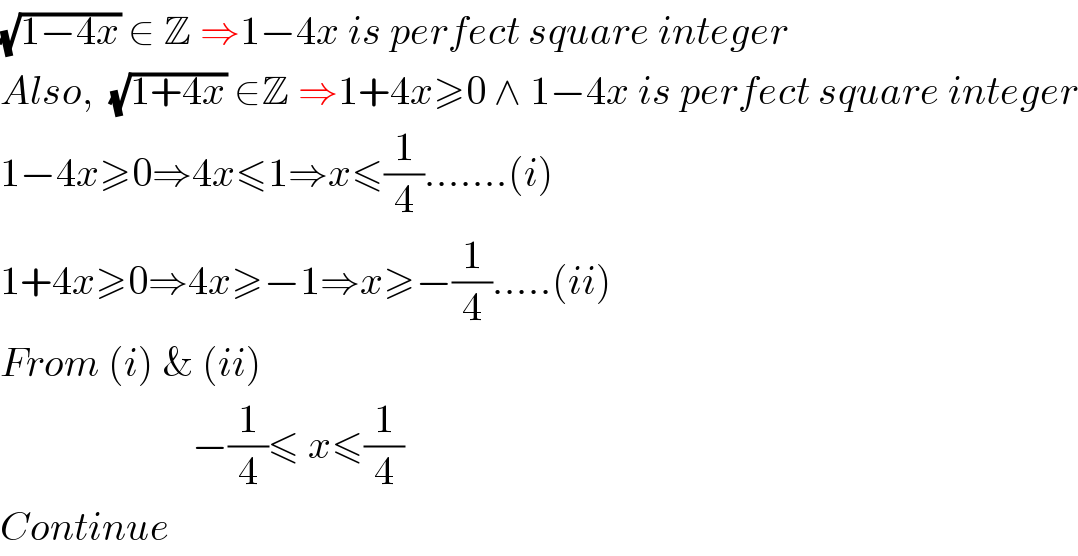
$$\sqrt{\mathrm{1}−\mathrm{4}{x}}\:\in\:\mathbb{Z}\:\Rightarrow\mathrm{1}−\mathrm{4}{x}\:{is}\:{perfect}\:{square}\:{integer} \\ $$$${Also},\:\:\sqrt{\mathrm{1}+\mathrm{4}{x}}\:\in\mathbb{Z}\:\Rightarrow\mathrm{1}+\mathrm{4}{x}\geqslant\mathrm{0}\:\wedge\:\mathrm{1}−\mathrm{4}{x}\:{is}\:{perfect}\:{square}\:{integer} \\ $$$$\mathrm{1}−\mathrm{4}{x}\geqslant\mathrm{0}\Rightarrow\mathrm{4}{x}\leqslant\mathrm{1}\Rightarrow{x}\leqslant\frac{\mathrm{1}}{\mathrm{4}}.......\left({i}\right) \\ $$$$\mathrm{1}+\mathrm{4}{x}\geqslant\mathrm{0}\Rightarrow\mathrm{4}{x}\geqslant−\mathrm{1}\Rightarrow{x}\geqslant−\frac{\mathrm{1}}{\mathrm{4}}.....\left({ii}\right) \\ $$$${From}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{4}}\leqslant\:{x}\leqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${Continue} \\ $$
Answered by Rasheed Soomro last updated on 18/Mar/16
![∵ S_1 ,S_2 ∈Z ∴ 1−4x and 1+4x are perfect square positive integers. Also sum of such numbers is 2: [ (1−4x) +(1+4x)=2 ] 2 is the sum of 1 and 1, which are only perfect square positive integers. So 1−4x=1 & 1+4x=1 ⇒ x=0.](Q4865.png)
$$\because\:\:{S}_{\mathrm{1}} ,{S}_{\mathrm{2}} \in\mathbb{Z} \\ $$$$\therefore\:\mathrm{1}−\mathrm{4}{x}\:\:{and}\:\:\mathrm{1}+\mathrm{4}{x}\:{are}\:{perfect}\:{square}\: \\ $$$${positive}\:{integers}. \\ $$$${Also}\:{sum}\:{of}\:{such}\:{numbers}\:{is}\:\mathrm{2}: \\ $$$$\:\:\:\:\:\:\left[\:\left(\mathrm{1}−\mathrm{4}{x}\right)\:+\left(\mathrm{1}+\mathrm{4}{x}\right)=\mathrm{2}\:\right] \\ $$$$\mathrm{2}\:{is}\:{the}\:{sum}\:{of}\:\mathrm{1}\:{and}\:\mathrm{1},\:{which}\:{are}\:{only}\:{perfect} \\ $$$${square}\:{positive}\:\:{integers}. \\ $$$${So}\:\mathrm{1}−\mathrm{4}{x}=\mathrm{1}\:\&\:\mathrm{1}+\mathrm{4}{x}=\mathrm{1}\:\Rightarrow\:{x}=\mathrm{0}. \\ $$
