
Question Number 48268 by ajfour last updated on 21/Nov/18
Commented by ajfour last updated on 21/Nov/18
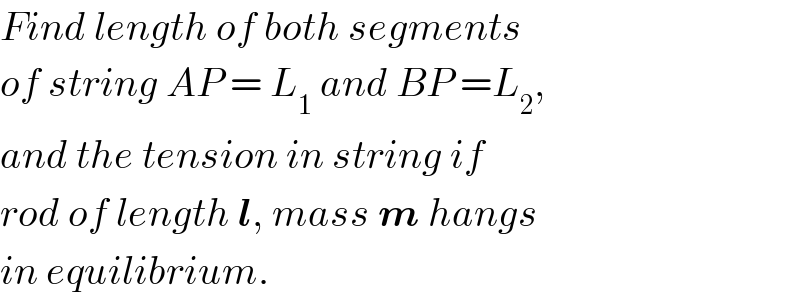
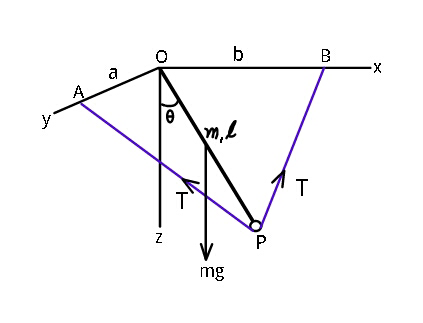
$${Find}\:{length}\:{of}\:{both}\:{segments} \\ $$$${of}\:{string}\:{AP}\:=\:{L}_{\mathrm{1}} \:{and}\:{BP}\:={L}_{\mathrm{2}} , \\ $$$${and}\:{the}\:{tension}\:{in}\:{string}\:{if} \\ $$$${rod}\:{of}\:{length}\:\boldsymbol{{l}},\:{mass}\:\boldsymbol{{m}}\:{hangs} \\ $$$${in}\:{equilibrium}. \\ $$
Commented by mr W last updated on 21/Nov/18
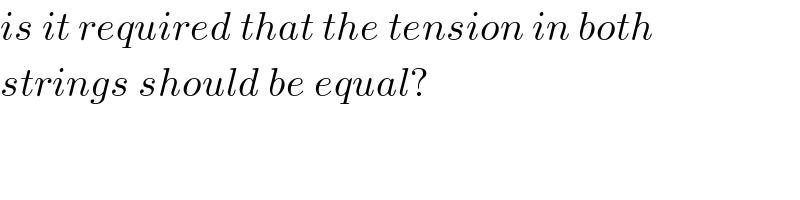
$${is}\:{it}\:{required}\:{that}\:{the}\:{tension}\:{in}\:{both} \\ $$$${strings}\:{should}\:{be}\:{equal}? \\ $$
Commented by ajfour last updated on 21/Nov/18
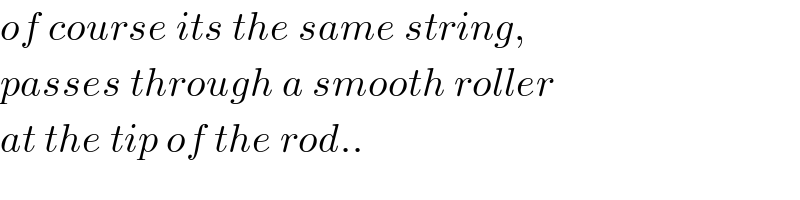
$${of}\:{course}\:{its}\:{the}\:{same}\:{string}, \\ $$$${passes}\:{through}\:{a}\:{smooth}\:{roller} \\ $$$${at}\:{the}\:{tip}\:{of}\:{the}\:{rod}.. \\ $$
Commented by mr W last updated on 21/Nov/18

$${I}\:{see}. \\ $$
Answered by mr W last updated on 21/Nov/18
Commented by mr W last updated on 27/Nov/18
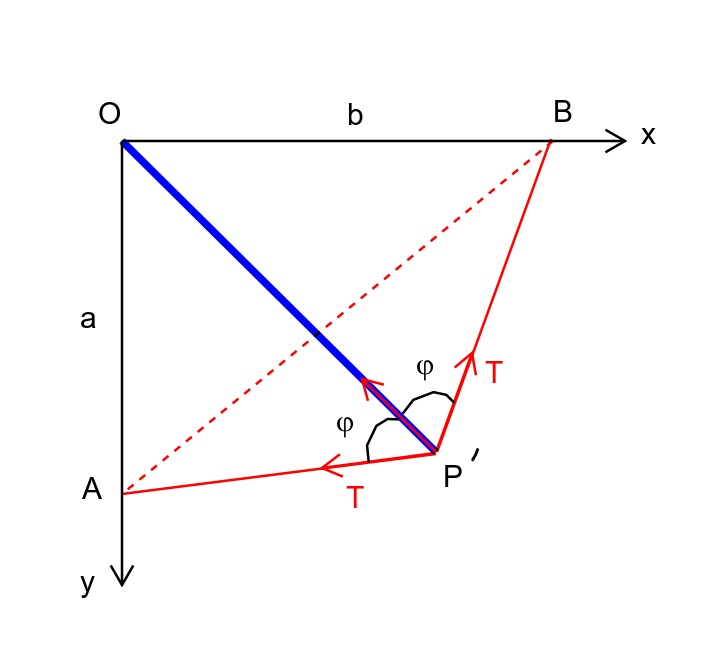
![OP′=l sin θ=l_1 ∠AOP′=α (a/(sin ϕ))=(l_1 /(sin (α+ϕ))) ...(i) (b/(sin ϕ))=(l_1 /(sin ((π/2)−α+ϕ)))=(l_1 /(cos (α−ϕ))) ...(ii) ⇒b cos (α−ϕ)=a sin (α+ϕ) ⇒b(cos α cos ϕ+sin α sin ϕ)=a(sin α cos ϕ+cos α sin ϕ) ⇒b(1+tan α tan ϕ)=a(tan α+ tan ϕ) ⇒(b tan ϕ−a)tan α=a tan ϕ−b ⇒tan α=((b−a tan ϕ)/(a−b tan ϕ)) ...(iii) sin α=((b−a tan ϕ)/(√((a^2 +b^2 )(1+tan^2 ϕ)−4ab tan ϕ))) cos α=((a−b tan ϕ)/(√((a^2 +b^2 )(1+tan^2 ϕ)−4ab tan ϕ))) from (i): ((sin α)/(tan ϕ))+cos α=(l_1 /a)=((l sin θ)/a) (1/(√((a^2 +b^2 )(1+tan^2 ϕ)−4ab tan ϕ)))[((b−a tan ϕ)/(tan ϕ))+a−b tan ϕ]=((l sin θ)/a) ⇒((ab)/(l(√((a^2 +b^2 )(1+tan^2 ϕ)−4ab tan ϕ))))((1/(tan ϕ))−tan ϕ)=sin θ we get ϕ from this eqn. then we get α from (iii). AP′=((a sin α)/(sin ϕ)) ⇒L_1 =(√((l cos θ)^2 +(((a sin α)/(sin ϕ)))^2 )) BP′=((b cos α)/(sin ϕ)) ⇒L_2 =(√((l cos θ)^2 +(((b cos α)/(sin ϕ)))^2 )) ⇒T=((mg)/(2[(1/(√(1+(((a sin α)/(l cos θ sin ϕ)))^2 )))+(1/(√(1+(((b cos α)/(l cos θ sin ϕ)))^2 )))])) ================= (b tan α−a) tan ϕ=a tan α−b ⇒tan ϕ=((a tan α−b)/(b tan α−a)) ⇒sin α (((b/a) tan α−1)/(tan α−(b/a)))+cos α=((l sin θ)/a)](Q48280.png)
$${OP}'={l}\:\mathrm{sin}\:\theta={l}_{\mathrm{1}} \\ $$$$\angle{AOP}'=\alpha \\ $$$$\frac{{a}}{\mathrm{sin}\:\varphi}=\frac{{l}_{\mathrm{1}} }{\mathrm{sin}\:\left(\alpha+\varphi\right)}\:\:\:...\left({i}\right) \\ $$$$\frac{{b}}{\mathrm{sin}\:\varphi}=\frac{{l}_{\mathrm{1}} }{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\alpha+\varphi\right)}=\frac{{l}_{\mathrm{1}} }{\mathrm{cos}\:\left(\alpha−\varphi\right)}\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow{b}\:\mathrm{cos}\:\left(\alpha−\varphi\right)={a}\:\mathrm{sin}\:\left(\alpha+\varphi\right) \\ $$$$\Rightarrow{b}\left(\mathrm{cos}\:\alpha\:\mathrm{cos}\:\varphi+\mathrm{sin}\:\alpha\:\mathrm{sin}\:\varphi\right)={a}\left(\mathrm{sin}\:\alpha\:\mathrm{cos}\:\varphi+\mathrm{cos}\:\alpha\:\mathrm{sin}\:\varphi\right) \\ $$$$\Rightarrow{b}\left(\mathrm{1}+\mathrm{tan}\:\alpha\:\mathrm{tan}\:\varphi\right)={a}\left(\mathrm{tan}\:\alpha+\:\mathrm{tan}\:\varphi\right) \\ $$$$\Rightarrow\left({b}\:\mathrm{tan}\:\varphi−{a}\right)\mathrm{tan}\:\alpha={a}\:\mathrm{tan}\:\varphi−{b} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{{b}−{a}\:\mathrm{tan}\:\varphi}{{a}−{b}\:\mathrm{tan}\:\varphi}\:\:\:...\left({iii}\right) \\ $$$$\mathrm{sin}\:\alpha=\frac{{b}−{a}\:\mathrm{tan}\:\varphi}{\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\varphi\right)−\mathrm{4}{ab}\:\mathrm{tan}\:\varphi}} \\ $$$$\mathrm{cos}\:\alpha=\frac{{a}−{b}\:\mathrm{tan}\:\varphi}{\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\varphi\right)−\mathrm{4}{ab}\:\mathrm{tan}\:\varphi}} \\ $$$$ \\ $$$${from}\:\left({i}\right): \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{tan}\:\varphi}+\mathrm{cos}\:\alpha=\frac{{l}_{\mathrm{1}} }{{a}}=\frac{{l}\:\mathrm{sin}\:\theta}{{a}} \\ $$$$\frac{\mathrm{1}}{\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\varphi\right)−\mathrm{4}{ab}\:\mathrm{tan}\:\varphi}}\left[\frac{{b}−{a}\:\mathrm{tan}\:\varphi}{\mathrm{tan}\:\varphi}+{a}−{b}\:\mathrm{tan}\:\varphi\right]=\frac{{l}\:\mathrm{sin}\:\theta}{{a}} \\ $$$$\Rightarrow\frac{{ab}}{{l}\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\varphi\right)−\mathrm{4}{ab}\:\mathrm{tan}\:\varphi}}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}−\mathrm{tan}\:\varphi\right)=\mathrm{sin}\:\theta \\ $$$${we}\:{get}\:\varphi\:{from}\:{this}\:{eqn}. \\ $$$${then}\:{we}\:{get}\:\alpha\:{from}\:\left({iii}\right). \\ $$$${AP}'=\frac{{a}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\varphi} \\ $$$$\Rightarrow{L}_{\mathrm{1}} =\sqrt{\left({l}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left(\frac{{a}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\varphi}\right)^{\mathrm{2}} } \\ $$$${BP}'=\frac{{b}\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\varphi} \\ $$$$\Rightarrow{L}_{\mathrm{2}} =\sqrt{\left({l}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left(\frac{{b}\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\varphi}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{T}=\frac{{mg}}{\mathrm{2}\left[\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\left(\frac{{a}\:\mathrm{sin}\:\alpha}{{l}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi}\right)^{\mathrm{2}} }}+\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\left(\frac{{b}\:\mathrm{cos}\:\alpha}{{l}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi}\right)^{\mathrm{2}} }}\right]} \\ $$$$================= \\ $$$$\left({b}\:\mathrm{tan}\:\alpha−{a}\right)\:\mathrm{tan}\:\varphi={a}\:\mathrm{tan}\:\alpha−{b} \\ $$$$\Rightarrow\mathrm{tan}\:\varphi=\frac{{a}\:\mathrm{tan}\:\alpha−{b}}{{b}\:\mathrm{tan}\:\alpha−{a}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha\:\frac{\frac{{b}}{{a}}\:\mathrm{tan}\:\alpha−\mathrm{1}}{\mathrm{tan}\:\alpha−\frac{{b}}{{a}}}+\mathrm{cos}\:\alpha=\frac{{l}\:\mathrm{sin}\:\theta}{{a}} \\ $$
Commented by ajfour last updated on 21/Nov/18
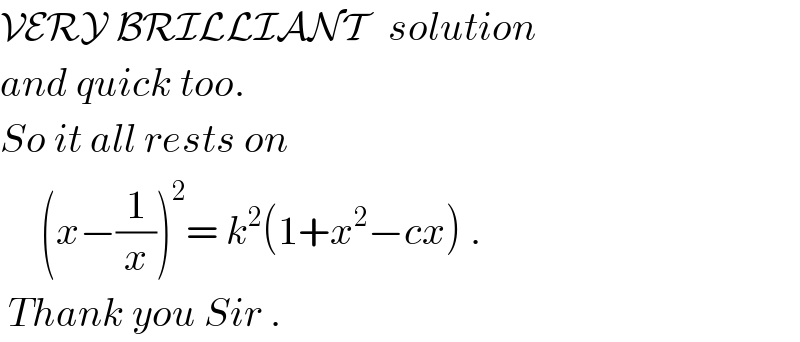
$$\mathcal{VERY}\:\mathcal{BRILLIANT}\:\:\:{solution} \\ $$$${and}\:{quick}\:{too}.\: \\ $$$${So}\:{it}\:{all}\:{rests}\:{on} \\ $$$$\:\:\:\:\:\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\:{k}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} −{cx}\right)\:. \\ $$$$\:{Thank}\:{you}\:{Sir}\:. \\ $$
Commented by ajfour last updated on 21/Nov/18
$${Understood}\:{every}\:{line}\:{Sir}. \\ $$
Commented by mr W last updated on 21/Nov/18
$${thanks}\:{for}\:{checking}\:{sir}! \\ $$
Commented by mr W last updated on 22/Nov/18
$${it}'{s}\:{more}\:{difficult}\:{if}\:{only}\:{the}\:{length} \\ $$$${of}\:{the}\:{string}\:{L}\:{is}\:{given},\:{not}\:{the}\:{angle} \\ $$$$\theta\:{for}\:{the}\:{rod}. \\ $$
