
Question Number 4825 by sanusihammed last updated on 16/Mar/16
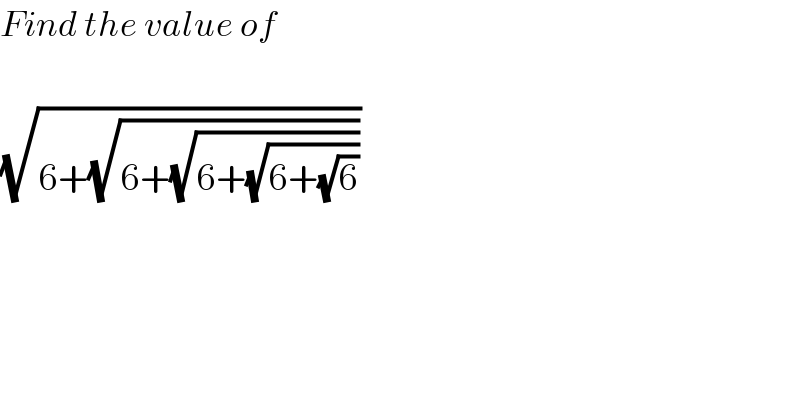
$${Find}\:{the}\:{value}\:{of}\: \\ $$$$ \\ $$$$\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}}}}}} \\ $$
Commented by prakash jain last updated on 16/Mar/16
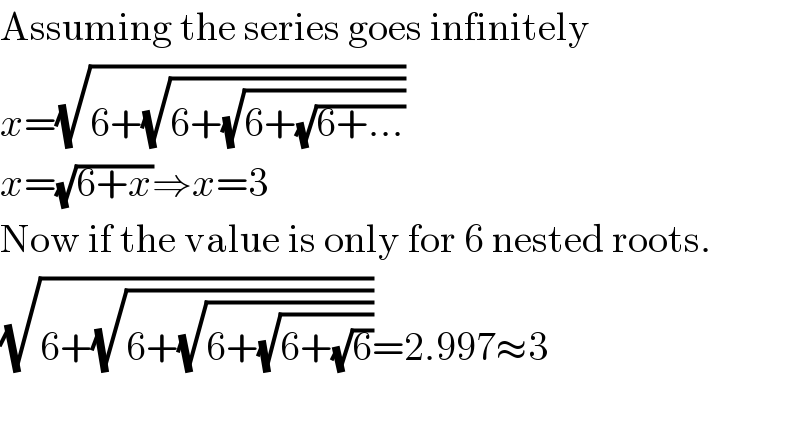
$$\mathrm{Assuming}\:\mathrm{the}\:\mathrm{series}\:\mathrm{goes}\:\mathrm{infinitely} \\ $$$${x}=\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+...}}}} \\ $$$${x}=\sqrt{\mathrm{6}+{x}}\Rightarrow{x}=\mathrm{3} \\ $$$$\mathrm{Now}\:\mathrm{if}\:\mathrm{the}\:\mathrm{value}\:\mathrm{is}\:\mathrm{only}\:\mathrm{for}\:\mathrm{6}\:\mathrm{nested}\:\mathrm{roots}. \\ $$$$\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}}}}}}=\mathrm{2}.\mathrm{997}\approx\mathrm{3} \\ $$$$ \\ $$
Commented by 123456 last updated on 16/Mar/16
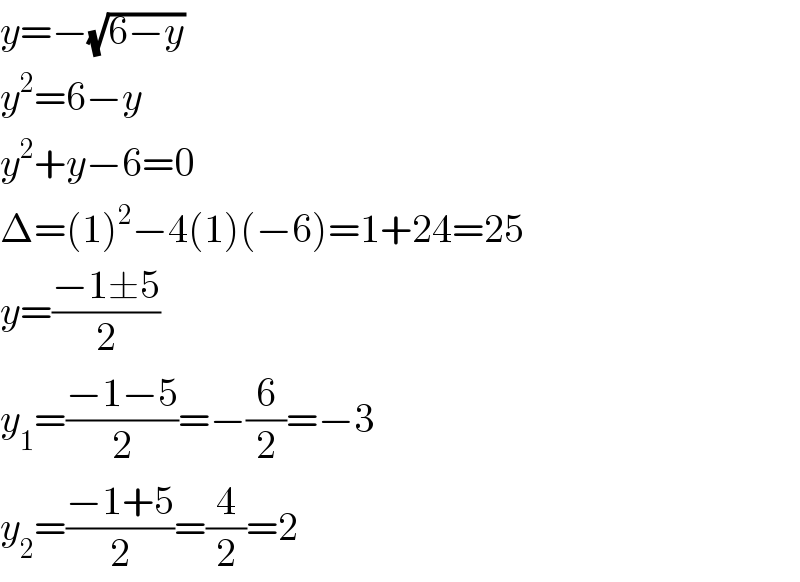
$${y}=−\sqrt{\mathrm{6}−{y}} \\ $$$${y}^{\mathrm{2}} =\mathrm{6}−{y} \\ $$$${y}^{\mathrm{2}} +{y}−\mathrm{6}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{6}\right)=\mathrm{1}+\mathrm{24}=\mathrm{25} \\ $$$${y}=\frac{−\mathrm{1}\pm\mathrm{5}}{\mathrm{2}} \\ $$$${y}_{\mathrm{1}} =\frac{−\mathrm{1}−\mathrm{5}}{\mathrm{2}}=−\frac{\mathrm{6}}{\mathrm{2}}=−\mathrm{3} \\ $$$${y}_{\mathrm{2}} =\frac{−\mathrm{1}+\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$
Answered by Rasheed Soomro last updated on 16/Mar/16

$${Let}\:{x}=\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}}}}}}.... \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}}}}}}..... \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} =\mathrm{6}+{x}\Rightarrow{x}^{\mathrm{2}} −{x}−\mathrm{6}=\mathrm{0} \\ $$$${x}=\frac{−\left(−\mathrm{1}\right)\pm\sqrt{\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{6}\right)}}{\mathrm{2}\left(\mathrm{1}\right)}=\frac{\mathrm{1}\pm\sqrt{\mathrm{25}}}{\mathrm{2}} \\ $$$${x}=\mathrm{3},−\mathrm{2} \\ $$$$−\mathrm{2}\:{is}\:{extraneous}\:{root}. \\ $$$$\therefore\:{x}=\mathrm{3} \\ $$
