
Question Number 48194 by Necxx last updated on 20/Nov/18
![A body of mass 0.1kg dropped from a height of 8m onto a hard floor bounces back to a height of 2m. Calculate the change of momentum. If the body is in contact with the floor for 0.1s then what is the force exerted on the body? [g=10ms^(−2) ]](Q48194.png)
$${A}\:{body}\:{of}\:{mass}\:\mathrm{0}.\mathrm{1}{kg}\:{dropped}\:{from} \\ $$$${a}\:{height}\:{of}\:\mathrm{8}{m}\:{onto}\:{a}\:{hard}\:{floor} \\ $$$${bounces}\:{back}\:{to}\:{a}\:{height}\:{of}\:\mathrm{2}{m}. \\ $$$${Calculate}\:{the}\:{change}\:{of}\:{momentum}. \\ $$$${If}\:{the}\:{body}\:{is}\:{in}\:{contact}\:{with}\:{the} \\ $$$${floor}\:{for}\:\mathrm{0}.\mathrm{1}{s}\:{then}\:{what}\:{is}\:{the} \\ $$$${force}\:{exerted}\:{on}\:{the}\:{body}? \\ $$$$\left[{g}=\mathrm{10}{ms}^{−\mathrm{2}} \right] \\ $$
Commented by Necxx last updated on 20/Nov/18

$${please}\:{help} \\ $$
Answered by mr W last updated on 21/Nov/18
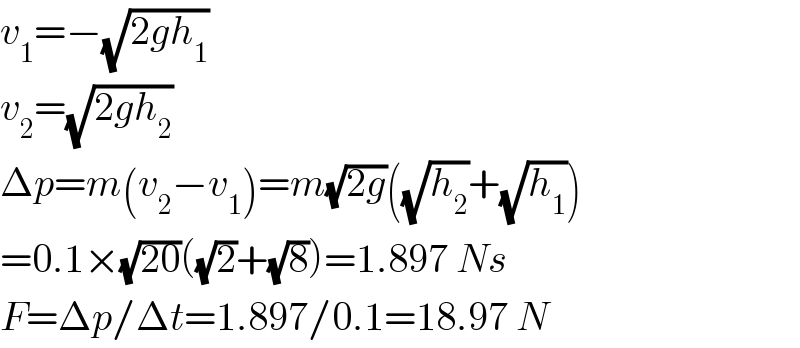
$${v}_{\mathrm{1}} =−\sqrt{\mathrm{2}{gh}_{\mathrm{1}} } \\ $$$${v}_{\mathrm{2}} =\sqrt{\mathrm{2}{gh}_{\mathrm{2}} } \\ $$$$\Delta{p}={m}\left({v}_{\mathrm{2}} −{v}_{\mathrm{1}} \right)={m}\sqrt{\mathrm{2}{g}}\left(\sqrt{{h}_{\mathrm{2}} }+\sqrt{{h}_{\mathrm{1}} }\right) \\ $$$$=\mathrm{0}.\mathrm{1}×\sqrt{\mathrm{20}}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{8}}\right)=\mathrm{1}.\mathrm{897}\:{Ns} \\ $$$${F}=\Delta{p}/\Delta{t}=\mathrm{1}.\mathrm{897}/\mathrm{0}.\mathrm{1}=\mathrm{18}.\mathrm{97}\:{N} \\ $$
Commented by Necxx last updated on 20/Nov/18

$${oh}.....\:{I}\:{thought}\:{its}\:{meant}\:{to}\:{be} \\ $$$${the}\:{difference}\:{between}\:{the}\:{final} \\ $$$${and}\:{initial}\:{momentum}\:{not}\:{the} \\ $$$${reverse}.{Why}\:{did}\:{you}\:{take}\:{this} \\ $$$${step}? \\ $$$$ \\ $$$${Thanks} \\ $$
Commented by Necxx last updated on 21/Nov/18
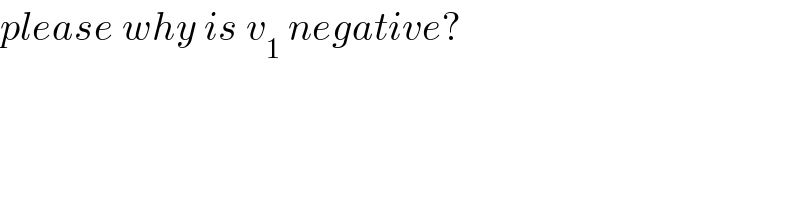
$${please}\:{why}\:{is}\:{v}_{\mathrm{1}} \:{negative}? \\ $$
Commented by mr W last updated on 21/Nov/18
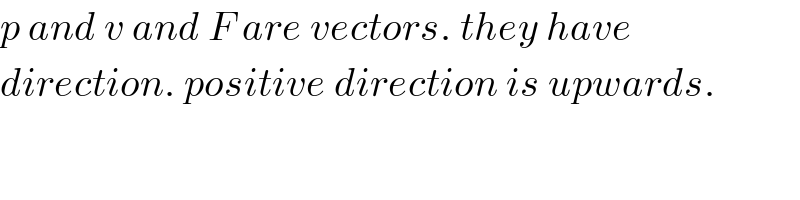
$${p}\:{and}\:{v}\:{and}\:{F}\:{are}\:{vectors}.\:{they}\:{have} \\ $$$${direction}.\:{positive}\:{direction}\:{is}\:{upwards}. \\ $$
Commented by Necxx last updated on 21/Nov/18
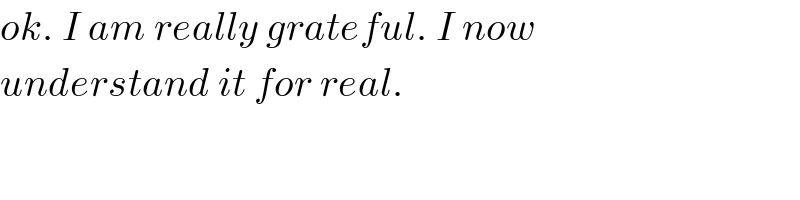
$${ok}.\:{I}\:{am}\:{really}\:{grateful}.\:{I}\:{now} \\ $$$${understand}\:{it}\:{for}\:{real}. \\ $$$$ \\ $$
