
Previous in Relation and Functions Next in Relation and Functions
Question Number 48169 by Abdo msup. last updated on 20/Nov/18
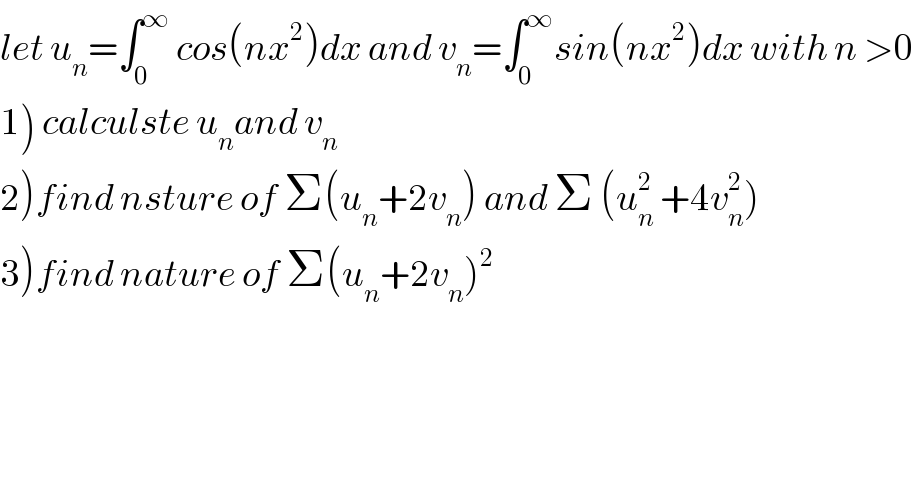
$${let}\:{u}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{cos}\left({nx}^{\mathrm{2}} \right){dx}\:{and}\:{v}_{{n}} =\int_{\mathrm{0}} ^{\infty} {sin}\left({nx}^{\mathrm{2}} \right){dx}\:{with}\:{n}\:>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right)\:{calculste}\:{u}_{{n}} {and}\:{v}_{{n}} \\ $$ $$\left.\mathrm{2}\right){find}\:{nsture}\:{of}\:\Sigma\left({u}_{{n}} +\mathrm{2}{v}_{{n}} \right)\:{and}\:\Sigma\:\left({u}_{{n}} ^{\mathrm{2}} \:+\mathrm{4}{v}_{{n}} ^{\mathrm{2}} \right) \\ $$ $$\left.\mathrm{3}\right){find}\:{nature}\:{of}\:\Sigma\left({u}_{{n}} +\mathrm{2}{v}_{{n}} \right)^{\mathrm{2}} \\ $$ $$ \\ $$
Commented bymaxmathsup by imad last updated on 23/Nov/18
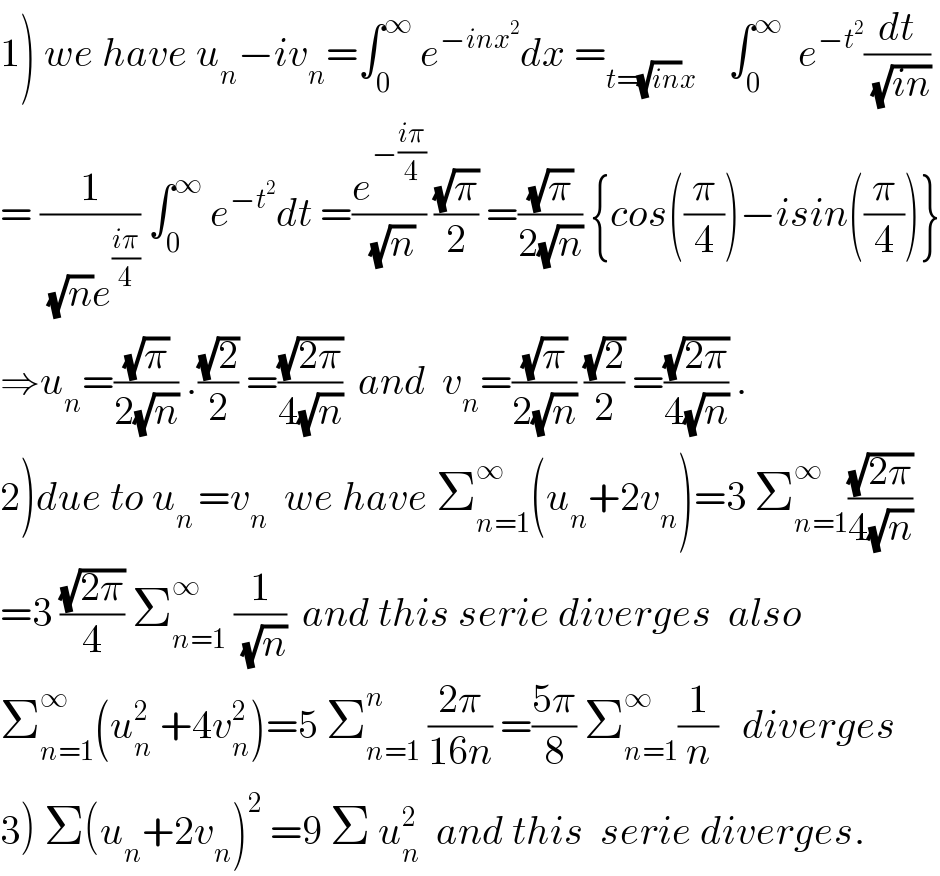
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{u}_{{n}} −{iv}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{e}^{−{inx}^{\mathrm{2}} } {dx}\:=_{{t}=\sqrt{{in}}{x}} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}^{\mathrm{2}} } \frac{{dt}}{\sqrt{{in}}} \\ $$ $$=\:\frac{\mathrm{1}}{\sqrt{{n}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:=\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{n}}}\:\frac{\sqrt{\pi}}{\mathrm{2}}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{{n}}}\:\left\{{cos}\left(\frac{\pi}{\mathrm{4}}\right)−{isin}\left(\frac{\pi}{\mathrm{4}}\right)\right\} \\ $$ $$\Rightarrow{u}_{{n}} =\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{{n}}}\:.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}\sqrt{{n}}}\:\:{and}\:\:{v}_{{n}} =\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{{n}}}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}\sqrt{{n}}}\:. \\ $$ $$\left.\mathrm{2}\right){due}\:{to}\:{u}_{{n}\:} ={v}_{{n}} \:\:{we}\:{have}\:\sum_{{n}=\mathrm{1}} ^{\infty} \left({u}_{{n}} +\mathrm{2}{v}_{{n}} \right)=\mathrm{3}\:\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}\sqrt{{n}}} \\ $$ $$=\mathrm{3}\:\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\sqrt{{n}}}\:\:{and}\:{this}\:{serie}\:{diverges}\:\:{also} \\ $$ $$\sum_{{n}=\mathrm{1}} ^{\infty} \left({u}_{{n}} ^{\mathrm{2}} \:+\mathrm{4}{v}_{{n}} ^{\mathrm{2}} \right)=\mathrm{5}\:\sum_{{n}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}\pi}{\mathrm{16}{n}}\:=\frac{\mathrm{5}\pi}{\mathrm{8}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}}\:\:\:{diverges} \\ $$ $$\left.\mathrm{3}\right)\:\Sigma\left({u}_{{n}} +\mathrm{2}{v}_{{n}} \right)^{\mathrm{2}} \:=\mathrm{9}\:\Sigma\:{u}_{{n}} ^{\mathrm{2}} \:\:{and}\:{this}\:\:{serie}\:{diverges}. \\ $$
